Part 1 Chain Rule
ถ้ามีสมการ
เราอาจเขียนใหม่ได้เป็น
แปลความออกมาในรูปของ computational graph ก็จะได้
ถ้ากำหนดให้ a = 1, b = 2, c = 3 แล้วท่อง graph นี้จากซ้ายไปขวา หรือ เรียกว่าแบบ "feed forward" ผลลัพธ์หรือค่าของ y จะเป็น 9
ที่นี้กลับมามองในมุมมองของการ train neural network บ้าง หากค่าที่ได้จากการสังเกตุจริง ค่าของ y เป็น 12 (ในขณะที่ค่าจากการคำนวณเป็น 9) เราจะสามารถคำนวนค่าความผิดพลาดนี้ได้จาก
ความผิดพลาดนี้ย่อมมาจากความผิดพลาดของ x และ c แต่จะโทษแต่ x และ c ไม่ได้ เพราะ x เกิดจาก a และ b ด้วย ดังนั้นควรแบ่งความรับผิดชอบกันไปทั่วหน้า เริ่มต้นต้้งแต่ปลายทางย้อนกลับไปยังจุดเริ่มต้น เรียกวิธีการคิดแบบนี้ว่า feed backward หรือ back propagation แต่จะให้รับผิดชอบกันอย่างไร เราใช้หล้กการของ partial derivative มาช่วย
ทำนองเดียวกันจะได้
และ X = a + b ดังนั้น คำถามต่อไปคือ \( \large \frac{\partial e}{\partial a} = ? \text{,}\frac{\partial e}{\partial b} = ?\)
คำตอบคือ "chain rule"
\( \large \frac{\partial e}{\partial a} = c\cdot\frac{\partial (a+b)}{\partial a} \)
\( \large \frac{\partial e}{\partial a} = c\cdot \left[\frac{\partial a}{\partial a} +\frac{\partial b}{\partial a} \right] \)
\(\large \frac{\partial e}{\partial a} = c\)
และทำนองเดียวกัน
บทบาทของ Chain rules อาจพอสรุปได้ตามแผนภาพต่อไปนี้
Part 2 Convolution
ความหมายของ Convolution จาก Wiki :
"In mathematics (and, in particular, functional analysis) convolution is a mathematical operation on two functions (f and g) to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it."
ถ้าเรามี 2 Matrix คือ X ขนาด 5x5 และ W ขนาด 3x3 ซึ่งจะเรียก X ว่าเป็น matrix ของข้อมูลที่จะถูกนำมาทำ convolution กับ matrix W
เราจะนิยาม matrix O ซึ่งเป็นผลลัพธ์จากการทำ convolution ระหว่าง X กับ W ดังนี้
โดย
\( \large O_{13} = X_{13}\cdot W_{11} +X_{14}\cdot W_{12}+X_{15}\cdot W_{13}\\ + \large X_{23}\cdot W_{21}+X_{24}\cdot W_{22}+X_{25}\cdot W_{23}\\+ \large X_{33}\cdot W_{32}+X_{34}\cdot W_{32}+X_{35}\cdot W_{33}\)
\( \large O_{21} = X_{21}\cdot W_{11} +X_{22}\cdot W_{12}+X_{23}\cdot W_{13}\\ + \large X_{31}\cdot W_{21}+X_{32}\cdot W_{22}+X_{33}\cdot W_{23}\\+ \large X_{41}\cdot W_{32}+X_{42}\cdot W_{32}+X_{43}\cdot W_{33}\)
\(\large O_{22} = X_{22}\cdot W_{11} +X_{23}\cdot W_{12}+X_{24}\cdot W_{13}\\ + \large X_{32}\cdot W_{21}+X_{33}\cdot W_{22}+X_{34}\cdot W_{23}\\+ \large X_{42}\cdot W_{32}+X_{42}\cdot W_{32}+X_{44}\cdot W_{33} \)
\( \large O_{23} = X_{23}\cdot W_{11} +X_{24}\cdot W_{12}+X_{25}\cdot W_{13}\\ + \large X_{33}\cdot W_{21}+X_{34}\cdot W_{22}+X_{35}\cdot W_{23}\\+ \large X_{43}\cdot W_{32}+X_{44}\cdot W_{32}+X_{45}\cdot W_{33}\)
\( \large O_{31} = X_{31}\cdot W_{11} +X_{32}\cdot W_{12}+X_{33}\cdot W_{13}\\ + \large X_{41}\cdot W_{21}+X_{42}\cdot W_{22}+X_{43}\cdot W_{23}\\+ \large X_{51}\cdot W_{32}+X_{52}\cdot W_{32}+X_{53}\cdot W_{33}\)
\(\large O_{32} = X_{32}\cdot W_{11} +X_{33}\cdot W_{12}+X_{34}\cdot W_{13}\\ + \large X_{42}\cdot W_{21}+X_{43}\cdot W_{22}+X_{44}\cdot W_{23}\\+ \large X_{52}\cdot W_{32}+X_{53}\cdot W_{32}+X_{54}\cdot W_{33} \)
\( \large O_{33} = X_{33}\cdot W_{11} +X_{34}\cdot W_{12}+X_{35}\cdot W_{13}\\ + \large X_{43}\cdot W_{21}+X_{44}\cdot W_{22}+X_{45}\cdot W_{23}\\+ \large X_{53}\cdot W_{32}+X_{54}\cdot W_{32}+X_{55}\cdot W_{33}\)
อาจสรุปขั้นตอนการทำ convolution มีลำดับดังนี้
1. เริ่มต้นที่ตำแหน่งมุมขวาบนของทั้ง matrix X และ W
2. หา element - wise multiplication ระหว่าง X และ W
3. นำลัพธ์จากข้อ 2 มาหาผลบวก จะได้ค่าของ Oij
4. ขยับ W ไปทางขวาของ X แล้วทำซ้ำข้อ 2 -3 จำนวนตำแหน่งที่ขยับไปทางขวาเรียกว่า stride
5. เมื่อขยับไปทางขวาจนสุดแล้ว ให้กลับมาเริ่มจากซ้ายสุดและขยับตำแหน่งลงมาข้างล่าง จำนวนที่ขยับลงเท่ากับ stride
6. ทำซ้ำข้อ 2 - 5 จนหมดจำนวนสมาชิกของ X
Part 3 Back Propagation
ปัญหาที่ค้างมาจาก Part 1 คือเราจะหา local gradient ของ X, และ W เพื่อนำไปสู่การหาค่า global gradient เทียบกับ X,W ได้จะต้องเริ่มต้นด้วยการหา partial derivative ของ output เทียบกับ X และ W ก่อน ซึ่งใน Part 2 เราก็ได้ทราบว่า output จากการทำ convolution ระหว่าง X, W ได้มาได้อย่างไร ใน Part 3 ก็จะนำเอาความรู้ทั้งหมดมาใช้เพื่อทำ Back propagation ของ Convolution Layer กัน
ยกตัวอย่าง
\( \large O_{11} = X_{11}\cdot W_{11} +X_{12}\cdot W_{12}+X_{13}\cdot W_{13}\\ + \large X_{21}\cdot W_{21}+X_{22}\cdot W_{22}+X_{23}\cdot W_{23}\\+ \large X_{31}\cdot W_{31}+X_{32}\cdot W_{32}+X_{33}\cdot W_{33}\)
ทำให้หา partial derivative ของ O11 เทียบกับ X11 ได้ดังนี้
\( \large \frac{\partial O_{11}}{\partial X_{11}} =
\frac{\partial (X_{11}\cdot W_{11})}{\partial X_{11}} +
\frac{\partial (X_{12}\cdot W_{12})}{\partial X_{11}}+
\frac{ \partial(X_{13}\cdot W_{13})}{\partial X_{11}}+
\frac{ \partial(X_{21}\cdot W_{21})}{\partial X_{11}}+
\frac{ \partial(X_{22}\cdot W_{22})}{\partial X_{11}}\\
\large + \frac{ \partial(X_{23}\cdot W_{23})}{\partial X_{11}}+
\frac{ \partial(X_{31}\cdot W_{31})}{\partial X_{11}}+
\frac{ \partial(X_{32}\cdot W_{32})}{\partial X_{11}}+
\frac{ \partial(X_{33}\cdot W_{33})}{\partial X_{11}} \)
ในทำนองเดียวกันเราก็จะสามารถหาค่า partial derivative อื่นได้ดังนี้
\( \large \frac{\partial O_{11}}{\partial X_{12}} = W_{12}\\ \large \frac{\partial O_{11}}{\partial X_{13}} = W_{13}\\ \large \frac{\partial O_{11}}{\partial X_{21}} = W_{21}\\ \large \frac{\partial O_{11}}{\partial X_{22}} = W_{22}\\ \large \frac{\partial O_{11}}{\partial X_{23}} = W_{23}\\ \large \frac{\partial O_{11}}{\partial X_{31}} = W_{31}\\ \large \frac{\partial O_{11}}{\partial X_{32}} = W_{32}\\ \large \frac{\partial O_{11}}{\partial X_{33}} = W_{33}\\\)
\(
\large \frac{\partial O_{11}}{\partial W_{11}} = X_{11}\\ \large \frac{\partial O_{11}}{\partial W_{12}} = X_{12}\\ \large \frac{\partial O_{11}}{\partial W_{13}} = X_{13}\\ \large \frac{\partial O_{11}}{\partial W_{21}} = X_{21}\\ \large \frac{\partial O_{11}}{\partial W_{22}} = X_{22}\\ \large \frac{\partial O_{11}}{\partial W_{23}} = X_{23}\\ \large \frac{\partial O_{11}}{\partial W_{31}} = X_{31}\\ \large \frac{\partial O_{11}}{\partial W_{32}} = X_{32}\\ \large \frac{\partial O_{11}}{\partial W_{33}} = X_{33}\\ \)
...
ค่า global gradient เทียบกับ \( W\)
\( \large \frac{\partial L}{\partial W_{11}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{11}} + \frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{11}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{11}}
\)
\( \large \frac{\partial L}{\partial W_{12}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{12}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{12}}
\)
\( \large \frac{\partial L}{\partial W_{13}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{13}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{13}}
\)
\( \large \frac{\partial L}{\partial W_{21}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{21}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{21}}
\)
จากความรู้ก่อนหน้านี้ทำให้เราสามารถเขียนสมการนี้ทั้งหมดได้เป็น
\( \frac{\partial L}{\partial W_{11}} = \frac{\partial L}{\partial O_{11}} \cdot X_{11}+ \frac{\partial L}{\partial O_{12}} \cdot X_{12} + \frac{\partial L}{\partial O_{13}} \cdot X_{13}+ \frac{\partial L}{\partial O_{21}} \cdot X_{21} + \frac{\partial L}{\partial O_{22}} \cdot X_{22} + \frac{\partial L}{\partial O_{23}} \cdot X_{23} +\\ \frac{\partial L}{\partial O_{31}} \cdot X_{31} + \frac{\partial L}{\partial O_{32}} \cdot X_{32}+ \frac{\partial L}{\partial O_{33}} \cdot X_{33}\)
....
หากสังเกตุให้ดีจะเห็นว่าการหาผลลัพธ์ที่ได้มีลักษณะเช่นเดียวกันการใช้ convolution นั้นคือ
\(\frac{\partial L}{\partial W} = \begin{bmatrix} X_{11} & X_{12} & X_{13}& X_{14}& X_{15} \\ X_{21} & X_{22} & X_{23}& X_{24}& X_{25} \\ X_{31} & X_{32} & X_{33} & X_{34} & X_{35} \\ X_{41} & X_{42} & X_{43} & X_{44} & X_{45} \\ X_{51} & X_{52} & X_{53} & X_{54} & X_{55} \end{bmatrix} \otimes \begin{bmatrix} \frac{\partial L}{\partial O_{11}} & \frac{\partial L}{\partial O_{12}} & \frac{\partial L}{\partial O_{13}} \\ \frac{\partial L}{\partial O_{21}} & \frac{\partial L}{\partial O_{22}} & \frac{\partial L}{\partial O_{23}} \\ \frac{\partial L}{\partial O_{31}} & \frac{\partial L}{\partial O_{32}} & \frac{\partial L}{\partial O_{33}} \\ \end{bmatrix} \dashrightarrow(1)\)
ในการหาค่า \( \large \frac{\partial L}{\partial X}\) ก็จะใช้การเดียวกัน ซึ่งจะละไว้ไม่ลงในรายละเอียด เพราะมันจะยืดยาวมาก แต่ก็ขอสรุปไว้ดังนี้
\( \frac{\partial L}{\partial X} = \begin{bmatrix} W_{33} & W_{32} & W_{31}\\ W_{23} & W_{22} & W_{21}\\ W_{13} & W_{12} & W_{11} \end{bmatrix} \otimes \begin{bmatrix} \frac{\partial L}{\partial O_{11}} & \frac{\partial L}{\partial O_{12}} & \frac{\partial L}{\partial O_{13}} \\ \frac{\partial L}{\partial O_{21}} & \frac{\partial L}{\partial O_{22}} & \frac{\partial L}{\partial O_{23}} \\ \frac{\partial L}{\partial O_{31}} & \frac{\partial L}{\partial O_{32}} & \frac{\partial L}{\partial O_{33}} \\ \end{bmatrix}\dashrightarrow(2) \)
หรือสรุปเป็นรูปแบบที่จำง่ายดังนี้
หมายเหตุ
1. การ rotate180 ในที่นี้คือการ flip matrix 2 ครั้ง ครั้งแรก flip แนวตั้ง ครั้งที่สอง flip แนวนอน
3. การทำ convolution ระหว่าง X และ global gradient จะกำหนดให้ padding = 0 และ stride = 1
4. ใช้หลักการ \( W_{k} = W_{k-1} - \epsilon \frac{\partial L}{\partial W} \) เพื่อปรับค่า Weight
ข้อมูลอ้างอิง
[1] http://colah.github.io/posts/2014-07-Understanding-Convolutions/
[2] http://colah.github.io/posts/2015-08-Backprop/
[3] https://youtu.be/QJoa0JYaX1I
[4] https://youtu.be/r2-P1Fi1g60
[5] https://youtu.be/tIeHLnjs5U8
[6] https://www.cs.cmu.edu/~mgormley/courses/10601-s17/slides/lecture20-backprop.pdf
[7] http://neuralnetworksanddeeplearning.com/chap2.html
[8] https://www.reddit.com/r/math/comments/4ieenr/calculus_and_backpropagation/
[9] https://www.youtube.com/playlist?list=PL3FW7Lu3i5JvHM8ljYj-zLfQRF3EO8sYv
[10] https://youtu.be/i94OvYb6noo
[11] https://en.wikipedia.org/wiki/Chain_rule
[12] http://www.cs.columbia.edu/~mcollins/ff2.pdf
[13] https://www.mathsisfun.com/calculus/derivatives-introduction.html?ref=binfind.com/web
[14] https://www.mathsisfun.com/calculus/derivatives-partial.html
[15] https://en.wikipedia.org/wiki/Convolution
[16] https://en.wikipedia.org/wiki/Matrix_(mathematics)
[17] https://medium.freecodecamp.org/an-intuitive-guide-to-convolutional-neural-networks-260c2de0a050
ถ้ามีสมการ
\(\large y = c \times (a+b)\)
เราอาจเขียนใหม่ได้เป็น
\(\large x = a+b \)
\( y = c \times x\)
\( y = c \times x\)
แปลความออกมาในรูปของ computational graph ก็จะได้
ถ้ากำหนดให้ a = 1, b = 2, c = 3 แล้วท่อง graph นี้จากซ้ายไปขวา หรือ เรียกว่าแบบ "feed forward" ผลลัพธ์หรือค่าของ y จะเป็น 9
ที่นี้กลับมามองในมุมมองของการ train neural network บ้าง หากค่าที่ได้จากการสังเกตุจริง ค่าของ y เป็น 12 (ในขณะที่ค่าจากการคำนวณเป็น 9) เราจะสามารถคำนวนค่าความผิดพลาดนี้ได้จาก
\( \large e = 9 - 12 = -3 \)
ความผิดพลาดนี้ย่อมมาจากความผิดพลาดของ x และ c แต่จะโทษแต่ x และ c ไม่ได้ เพราะ x เกิดจาก a และ b ด้วย ดังนั้นควรแบ่งความรับผิดชอบกันไปทั่วหน้า เริ่มต้นต้้งแต่ปลายทางย้อนกลับไปยังจุดเริ่มต้น เรียกวิธีการคิดแบบนี้ว่า feed backward หรือ back propagation แต่จะให้รับผิดชอบกันอย่างไร เราใช้หล้กการของ partial derivative มาช่วย
\( \large e = cx - 12 \)
\(\large \frac{\partial e}{\partial x} = \frac{\partial cx }{\partial x} - \frac{\partial 12 }{\partial x} \)
\(\large \frac{\partial e}{\partial x} = c \)
\(\large \frac{\partial e}{\partial x} = \frac{\partial cx }{\partial x} - \frac{\partial 12 }{\partial x} \)
\(\large \frac{\partial e}{\partial x} = c \)
ทำนองเดียวกันจะได้
\(\large \frac{\partial e}{\partial c} = x \)
และ X = a + b ดังนั้น คำถามต่อไปคือ \( \large \frac{\partial e}{\partial a} = ? \text{,}\frac{\partial e}{\partial b} = ?\)
คำตอบคือ "chain rule"
\( \large \frac{\partial e}{\partial a} = \frac{\partial e}{\partial x}\cdot\frac{\partial x}{\partial a} \)
\( \large \frac{\partial e}{\partial a} = c\cdot\frac{\partial (a+b)}{\partial a} \)
\( \large \frac{\partial e}{\partial a} = c\cdot \left[\frac{\partial a}{\partial a} +\frac{\partial b}{\partial a} \right] \)
\(\large \frac{\partial e}{\partial a} = c\)
และทำนองเดียวกัน
\( \large \frac{\partial e}{\partial b} = \frac{\partial e}{\partial x}\cdot\frac{\partial x}{\partial b} \)
\( \large \frac{\partial e}{\partial b} = c \)บทบาทของ Chain rules อาจพอสรุปได้ตามแผนภาพต่อไปนี้
 |
| Data และ Weight ถูกนำเข้าไปใน Neuron เพื่อสร้าง Output (Z) หรือ f(X,W) = Z |
 |
| ขั้นตอนการทำ back propagation เริ่มต้นการหาคา local gradient ด้วย partial derivative ของทั้ง Data และ Weight |
 |
| คำนวณหาอิทธิพลของตัวแปรแต่ละตัวใน Neuron โดยการหาผลคูณระหว่าง global gradient กับ local gradient |
Part 2 Convolution
ความหมายของ Convolution จาก Wiki :
"In mathematics (and, in particular, functional analysis) convolution is a mathematical operation on two functions (f and g) to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it."
ถ้าเรามี 2 Matrix คือ X ขนาด 5x5 และ W ขนาด 3x3 ซึ่งจะเรียก X ว่าเป็น matrix ของข้อมูลที่จะถูกนำมาทำ convolution กับ matrix W
เราจะนิยาม matrix O ซึ่งเป็นผลลัพธ์จากการทำ convolution ระหว่าง X กับ W ดังนี้
\( \large O_{11} = X_{11}\cdot W_{11} +X_{12}\cdot W_{12}+X_{13}\cdot W_{13}\\ + \large X_{21}\cdot W_{21}+X_{22}\cdot W_{22}+X_{23}\cdot W_{23}\\+ \large X_{31}\cdot W_{31}+X_{32}\cdot W_{32}+X_{33}\cdot W_{33}\)
\(\large O_{12} = X_{12}\cdot W_{11} +X_{13}\cdot W_{12}+X_{14}\cdot W_{13}\\ + \large X_{22}\cdot W_{21}+X_{23}\cdot W_{22}+X_{24}\cdot W_{23}\\+ \large X_{32}\cdot W_{32}+X_{32}\cdot W_{32}+X_{34}\cdot W_{33} \)
\( \large O_{13} = X_{13}\cdot W_{11} +X_{14}\cdot W_{12}+X_{15}\cdot W_{13}\\ + \large X_{23}\cdot W_{21}+X_{24}\cdot W_{22}+X_{25}\cdot W_{23}\\+ \large X_{33}\cdot W_{32}+X_{34}\cdot W_{32}+X_{35}\cdot W_{33}\)
\( \large O_{21} = X_{21}\cdot W_{11} +X_{22}\cdot W_{12}+X_{23}\cdot W_{13}\\ + \large X_{31}\cdot W_{21}+X_{32}\cdot W_{22}+X_{33}\cdot W_{23}\\+ \large X_{41}\cdot W_{32}+X_{42}\cdot W_{32}+X_{43}\cdot W_{33}\)
\(\large O_{22} = X_{22}\cdot W_{11} +X_{23}\cdot W_{12}+X_{24}\cdot W_{13}\\ + \large X_{32}\cdot W_{21}+X_{33}\cdot W_{22}+X_{34}\cdot W_{23}\\+ \large X_{42}\cdot W_{32}+X_{42}\cdot W_{32}+X_{44}\cdot W_{33} \)
\( \large O_{23} = X_{23}\cdot W_{11} +X_{24}\cdot W_{12}+X_{25}\cdot W_{13}\\ + \large X_{33}\cdot W_{21}+X_{34}\cdot W_{22}+X_{35}\cdot W_{23}\\+ \large X_{43}\cdot W_{32}+X_{44}\cdot W_{32}+X_{45}\cdot W_{33}\)
\( \large O_{31} = X_{31}\cdot W_{11} +X_{32}\cdot W_{12}+X_{33}\cdot W_{13}\\ + \large X_{41}\cdot W_{21}+X_{42}\cdot W_{22}+X_{43}\cdot W_{23}\\+ \large X_{51}\cdot W_{32}+X_{52}\cdot W_{32}+X_{53}\cdot W_{33}\)
\(\large O_{32} = X_{32}\cdot W_{11} +X_{33}\cdot W_{12}+X_{34}\cdot W_{13}\\ + \large X_{42}\cdot W_{21}+X_{43}\cdot W_{22}+X_{44}\cdot W_{23}\\+ \large X_{52}\cdot W_{32}+X_{53}\cdot W_{32}+X_{54}\cdot W_{33} \)
\( \large O_{33} = X_{33}\cdot W_{11} +X_{34}\cdot W_{12}+X_{35}\cdot W_{13}\\ + \large X_{43}\cdot W_{21}+X_{44}\cdot W_{22}+X_{45}\cdot W_{23}\\+ \large X_{53}\cdot W_{32}+X_{54}\cdot W_{32}+X_{55}\cdot W_{33}\)
อาจสรุปขั้นตอนการทำ convolution มีลำดับดังนี้
1. เริ่มต้นที่ตำแหน่งมุมขวาบนของทั้ง matrix X และ W
2. หา element - wise multiplication ระหว่าง X และ W
3. นำลัพธ์จากข้อ 2 มาหาผลบวก จะได้ค่าของ Oij
4. ขยับ W ไปทางขวาของ X แล้วทำซ้ำข้อ 2 -3 จำนวนตำแหน่งที่ขยับไปทางขวาเรียกว่า stride
5. เมื่อขยับไปทางขวาจนสุดแล้ว ให้กลับมาเริ่มจากซ้ายสุดและขยับตำแหน่งลงมาข้างล่าง จำนวนที่ขยับลงเท่ากับ stride
6. ทำซ้ำข้อ 2 - 5 จนหมดจำนวนสมาชิกของ X
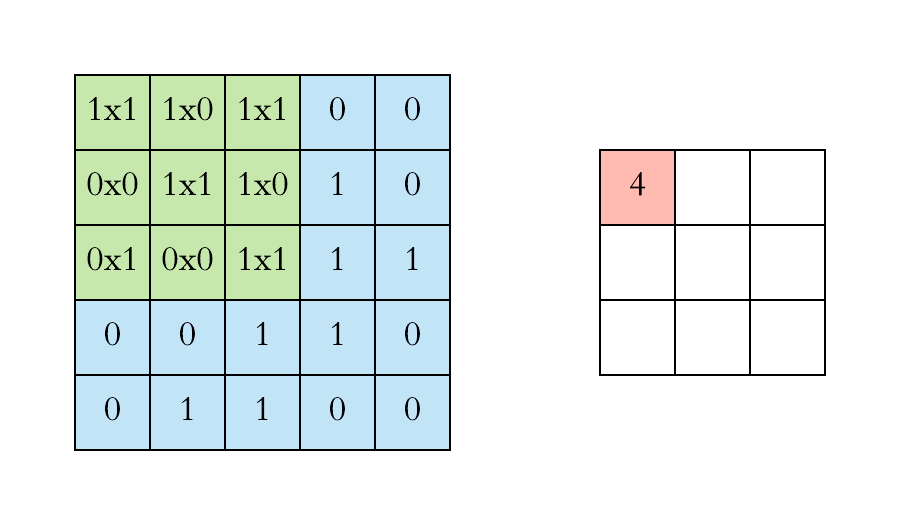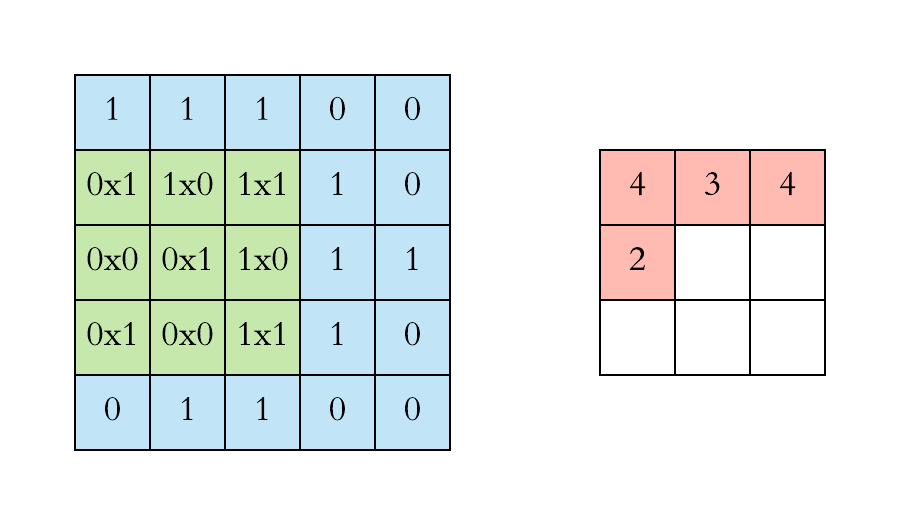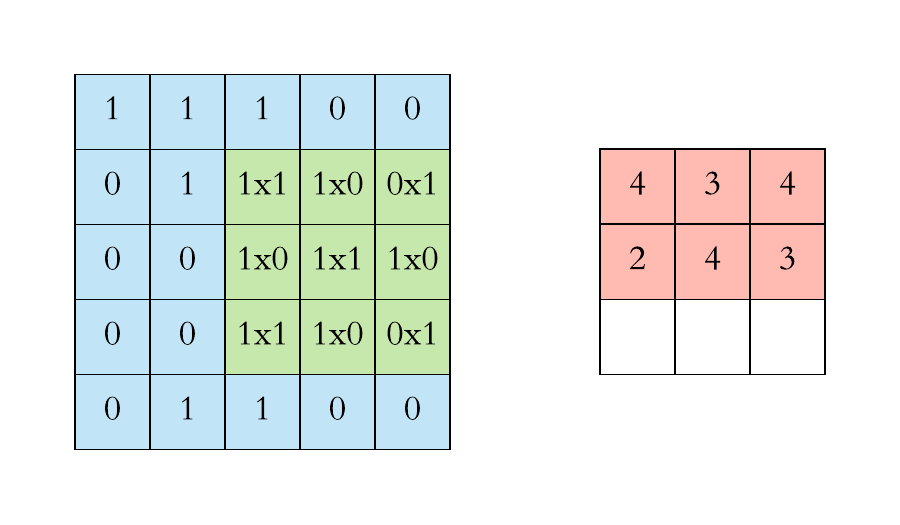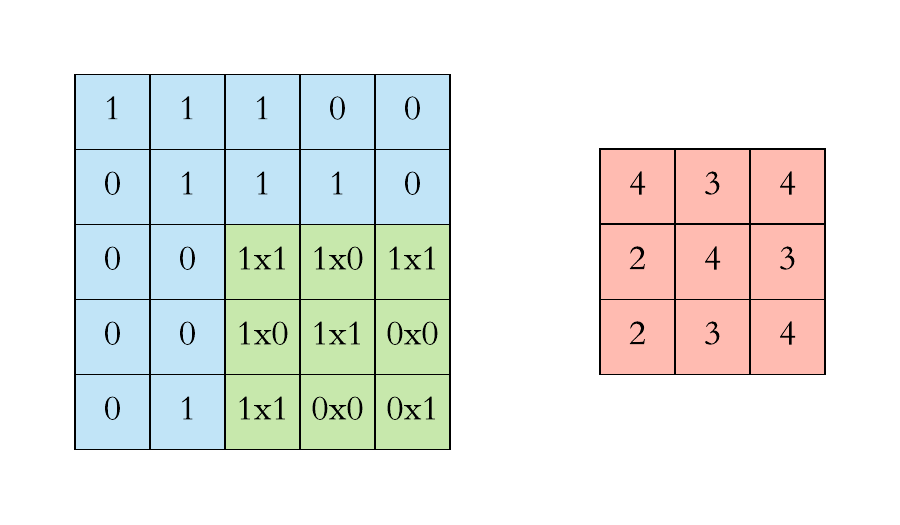 |
| ภาพจาก https://towardsdatascience.com/applied-deep-learning-part-4-convolutional-neural-networks-584bc134c1e2 |
Part 3 Back Propagation
ปัญหาที่ค้างมาจาก Part 1 คือเราจะหา local gradient ของ X, และ W เพื่อนำไปสู่การหาค่า global gradient เทียบกับ X,W ได้จะต้องเริ่มต้นด้วยการหา partial derivative ของ output เทียบกับ X และ W ก่อน ซึ่งใน Part 2 เราก็ได้ทราบว่า output จากการทำ convolution ระหว่าง X, W ได้มาได้อย่างไร ใน Part 3 ก็จะนำเอาความรู้ทั้งหมดมาใช้เพื่อทำ Back propagation ของ Convolution Layer กัน
ยกตัวอย่าง
ทำให้หา partial derivative ของ O11 เทียบกับ X11 ได้ดังนี้
\( \large \frac{\partial O_{11}}{\partial X_{11}} = W_{11} \)
ในทำนองเดียวกันเราก็จะสามารถหาค่า partial derivative อื่นได้ดังนี้
\( \large \frac{\partial O_{11}}{\partial X_{12}} = W_{12}\\ \large \frac{\partial O_{11}}{\partial X_{13}} = W_{13}\\ \large \frac{\partial O_{11}}{\partial X_{21}} = W_{21}\\ \large \frac{\partial O_{11}}{\partial X_{22}} = W_{22}\\ \large \frac{\partial O_{11}}{\partial X_{23}} = W_{23}\\ \large \frac{\partial O_{11}}{\partial X_{31}} = W_{31}\\ \large \frac{\partial O_{11}}{\partial X_{32}} = W_{32}\\ \large \frac{\partial O_{11}}{\partial X_{33}} = W_{33}\\\)
\(
\large \frac{\partial O_{11}}{\partial W_{11}} = X_{11}\\ \large \frac{\partial O_{11}}{\partial W_{12}} = X_{12}\\ \large \frac{\partial O_{11}}{\partial W_{13}} = X_{13}\\ \large \frac{\partial O_{11}}{\partial W_{21}} = X_{21}\\ \large \frac{\partial O_{11}}{\partial W_{22}} = X_{22}\\ \large \frac{\partial O_{11}}{\partial W_{23}} = X_{23}\\ \large \frac{\partial O_{11}}{\partial W_{31}} = X_{31}\\ \large \frac{\partial O_{11}}{\partial W_{32}} = X_{32}\\ \large \frac{\partial O_{11}}{\partial W_{33}} = X_{33}\\ \)
...
ค่า global gradient เทียบกับ \( W\)
\( \large \frac{\partial L}{\partial W_{11}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{11}} + \frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{11}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{11}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{11}}
\)
\( \large \frac{\partial L}{\partial W_{12}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{12}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{12}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{12}}
\)
\( \large \frac{\partial L}{\partial W_{13}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{13}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{13}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{13}}
\)
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{21}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{21}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{21}}
\)
\( \large \frac{\partial L}{\partial W_{22}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{22}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{22}}
\)
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{22}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{22}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{22}}
\)
\( \large \frac{\partial L}{\partial W_{23}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{23}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{23}}
\)
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{23}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{23}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{23}}
\)
\( \large \frac{\partial L}{\partial W_{31}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{31}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{31}}
\)
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{31}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{31}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{31}}
\)
\( \large \frac{\partial L}{\partial W_{31}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{32}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{32}}
\)
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{32}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{32}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{32}}
\)
\( \large \frac{\partial L}{\partial W_{33}} = \frac{\partial L}{\partial O_{11}} \cdot \frac{\partial O_{11}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{33}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{33}}
\)
...\frac{\partial L}{\partial O_{12}} \cdot \frac{\partial O_{12}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{13}} \cdot \frac{\partial O_{13}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{21}} \cdot \frac{\partial O_{21}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{22}} \cdot \frac{\partial O_{22}}{\partial W_{33}} + \\
\large \frac{\partial L}{\partial O_{23}} \cdot \frac{\partial O_{23}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{31}} \cdot \frac{\partial O_{31}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{32}} \cdot \frac{\partial O_{32}}{\partial W_{33}} +
\frac{\partial L}{\partial O_{33}} \cdot \frac{\partial O_{33}}{\partial W_{33}}
\)
จากความรู้ก่อนหน้านี้ทำให้เราสามารถเขียนสมการนี้ทั้งหมดได้เป็น
\( \frac{\partial L}{\partial W_{11}} = \frac{\partial L}{\partial O_{11}} \cdot X_{11}+ \frac{\partial L}{\partial O_{12}} \cdot X_{12} + \frac{\partial L}{\partial O_{13}} \cdot X_{13}+ \frac{\partial L}{\partial O_{21}} \cdot X_{21} + \frac{\partial L}{\partial O_{22}} \cdot X_{22} + \frac{\partial L}{\partial O_{23}} \cdot X_{23} +\\ \frac{\partial L}{\partial O_{31}} \cdot X_{31} + \frac{\partial L}{\partial O_{32}} \cdot X_{32}+ \frac{\partial L}{\partial O_{33}} \cdot X_{33}\)
....
หากสังเกตุให้ดีจะเห็นว่าการหาผลลัพธ์ที่ได้มีลักษณะเช่นเดียวกันการใช้ convolution นั้นคือ
\(\frac{\partial L}{\partial W} = \begin{bmatrix} X_{11} & X_{12} & X_{13}& X_{14}& X_{15} \\ X_{21} & X_{22} & X_{23}& X_{24}& X_{25} \\ X_{31} & X_{32} & X_{33} & X_{34} & X_{35} \\ X_{41} & X_{42} & X_{43} & X_{44} & X_{45} \\ X_{51} & X_{52} & X_{53} & X_{54} & X_{55} \end{bmatrix} \otimes \begin{bmatrix} \frac{\partial L}{\partial O_{11}} & \frac{\partial L}{\partial O_{12}} & \frac{\partial L}{\partial O_{13}} \\ \frac{\partial L}{\partial O_{21}} & \frac{\partial L}{\partial O_{22}} & \frac{\partial L}{\partial O_{23}} \\ \frac{\partial L}{\partial O_{31}} & \frac{\partial L}{\partial O_{32}} & \frac{\partial L}{\partial O_{33}} \\ \end{bmatrix} \dashrightarrow(1)\)
ในการหาค่า \( \large \frac{\partial L}{\partial X}\) ก็จะใช้การเดียวกัน ซึ่งจะละไว้ไม่ลงในรายละเอียด เพราะมันจะยืดยาวมาก แต่ก็ขอสรุปไว้ดังนี้
\( \frac{\partial L}{\partial X} = \begin{bmatrix} W_{33} & W_{32} & W_{31}\\ W_{23} & W_{22} & W_{21}\\ W_{13} & W_{12} & W_{11} \end{bmatrix} \otimes \begin{bmatrix} \frac{\partial L}{\partial O_{11}} & \frac{\partial L}{\partial O_{12}} & \frac{\partial L}{\partial O_{13}} \\ \frac{\partial L}{\partial O_{21}} & \frac{\partial L}{\partial O_{22}} & \frac{\partial L}{\partial O_{23}} \\ \frac{\partial L}{\partial O_{31}} & \frac{\partial L}{\partial O_{32}} & \frac{\partial L}{\partial O_{33}} \\ \end{bmatrix}\dashrightarrow(2) \)
หรือสรุปเป็นรูปแบบที่จำง่ายดังนี้
\(\large \frac{\partial L}{\partial X} = Rotate180(Weight) \otimes \frac{\partial L}{\partial O} \)
\(\large \frac{\partial L}{\partial W} = X \otimes \frac{\partial L}{\partial O} \)
หมายเหตุ
1. การ rotate180 ในที่นี้คือการ flip matrix 2 ครั้ง ครั้งแรก flip แนวตั้ง ครั้งที่สอง flip แนวนอน
import numpy as np
a = np.array([[1,2,3],[4,5,6],[7,8,9]])
b = np.flip(a,axis=1) # flip vertically
c = np.flip(b,axis=0) # flip horizontally
3. การทำ convolution ระหว่าง X และ global gradient จะกำหนดให้ padding = 0 และ stride = 1
4. ใช้หลักการ \( W_{k} = W_{k-1} - \epsilon \frac{\partial L}{\partial W} \) เพื่อปรับค่า Weight
ข้อมูลอ้างอิง
[1] http://colah.github.io/posts/2014-07-Understanding-Convolutions/
[2] http://colah.github.io/posts/2015-08-Backprop/
[3] https://youtu.be/QJoa0JYaX1I
[4] https://youtu.be/r2-P1Fi1g60
[5] https://youtu.be/tIeHLnjs5U8
[6] https://www.cs.cmu.edu/~mgormley/courses/10601-s17/slides/lecture20-backprop.pdf
[7] http://neuralnetworksanddeeplearning.com/chap2.html
[8] https://www.reddit.com/r/math/comments/4ieenr/calculus_and_backpropagation/
[9] https://www.youtube.com/playlist?list=PL3FW7Lu3i5JvHM8ljYj-zLfQRF3EO8sYv
[10] https://youtu.be/i94OvYb6noo
[11] https://en.wikipedia.org/wiki/Chain_rule
[12] http://www.cs.columbia.edu/~mcollins/ff2.pdf
[13] https://www.mathsisfun.com/calculus/derivatives-introduction.html?ref=binfind.com/web
[14] https://www.mathsisfun.com/calculus/derivatives-partial.html
[15] https://en.wikipedia.org/wiki/Convolution
[16] https://en.wikipedia.org/wiki/Matrix_(mathematics)
[17] https://medium.freecodecamp.org/an-intuitive-guide-to-convolutional-neural-networks-260c2de0a050






ความคิดเห็น
แสดงความคิดเห็น