Statistics : Covariance Matrix and Correlation Matrix

Covariance matrix

เป็นเครื่องมือที่ช่วยให้เข้าใจใน data set  บอกให้ทราบถึงขนาดของการกระจายตัวของข้อมูลผ่าน variance และทิศทางของความสัมพันธ์ระหว่างข้อมูลผ่าน covariance  ก่อนจะกล่าวถึงการสร้าง covariance matrix ต้องทบทวน สองเรื่องคือ variance คำนวณได้ตามสมการ (1) และ covariance คำนวณได้สมการที่ (2) 

\[ \begin{align*} \sigma^2_{x} &= \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})^2 \tag{1}\\\\ \sigma(x,y) &= \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y}) \tag{2.1}\\\\ Cov(x,y) &= \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y}) \tag{2.2}\\\\ \end{align*} \] หมายเหตุ : ใช้กรณีของ discreate


จาก (2.1) ถ้าเขียนในรูปของ vector จะได้ \[ Cov(\vec{x},\vec{y}) = \frac{1}{n-1} (\vec{x}-\bar{\vec{x}})^T (\vec{y}-\bar{\vec{y}}) \tag{2.3} \]

หากมีชุดของ vector \( \vec{x_1},\vec{x_2},\vec{x_3},...,\vec{x_p} \) แทนชุดข้อมูลจำนวน p ชุด แต่ละชุดมีข้อมูลจำนวน n ข้อมูล สร้าง matrix ได้ดังนี้ \[ X = \begin{bmatrix} | & | & | & ... & | \\ x_1 & x_2 & x_3 & ... & x_p \\ | & | & | & ... & | \\ \end{bmatrix} \] \[ Cov(X) = \frac{1}{n-1}(X^T \cdot X) \tag{2.4} \]

  covariance matrix คือการนำเอา covariance ที่ได้จากการจับคู่ของ data dimension เป็นไปได้ทั้งหมดมาสร้างเป็น square matrix สมมุติว่ามีข้อมูลสองมิติ X,Y covariance ที่เป็นไปได้คือ cov(X,X), cov(X,Y), cov(Y,Y) และ cov(Y,X) \[ \text{Covariance Matrix} = \begin{bmatrix} cov(X,X) & cov(X,Y) \\ cov(Y,X) & cov(Y,Y) \end{bmatrix} \tag{3} \]

พิจารณาดูโครงสร้างของ covariance matrix ในตัวอย่างจะพบว่า

1.  cov(X,X) และ cov(Y,Y) ซึ่งที่จริงแล้วก็คือ variance ของ X และ Y ตามลำดับ  ดังนั้น element ของ covariance matrix จึงประกอบด้วยทั้ง variance และ covariance  โดย variance จะเป็น element ที่อยู่ในแนวเส้นทะแยงมุม (diagonal) 

2.  cov(X,Y) ต้องเท่ากับ cov(Y,X) ทำให้เราทราบได้ว่า covariance matrix ต้อง symmetric  

3. จำนวน dimension จะเท่ากับ dimension ของข้อมูลที่มี ถ้ามีข้อมูล N dimension ก็จะใช้ \(N \times N \) matrix 

4. เราสามารถสรุปโครงสร้างของ Covariance Matrix คือ \[ \text{Cov Matrix} = \begin{bmatrix} \sigma_X^2 & \rho(X,Y) \\ \rho(Y,X) & \sigma_Y^2 \end{bmatrix} \tag{4} \]

ตัวอย่าง

สมมุติว่ามีนักเรียน 100 คน ทุกคนทำการทดสอบข้อเขียน 3 วิชาคือ คณิตศาสตร์, ภาษาอังกฤษและศิลปะ ทุกวิชามีคะแนนเต็ม 100 คะแนน ตัวอย่างคะแนนที่ได้คือ


คณิตศาสตร์ ภาษาอังกฤษ ศิลปะ
98 73 56
62 46 57
35 26 12
63 49 64
86 64 77
112 79 66
74 60 51
53 46 44
110 90 50
52 25 71
\( \vdots\) \( \vdots\) \( \vdots\)


คำนวณหา covariance  ตามขั้นตอนนี้

1. เปลี่ยนข้อมูลในตารางให้อยู่ในรูป matrix  \[ A = \begin{bmatrix} 98&73&56\\ 35&36&12\\ 63&49&64\\ \vdots&\vdots&\vdots\\ \end{bmatrix} \]


2. หาค่าเฉลี่ยของแต่ละ dimension (วิชา / column) \[ \bar{X} = \frac{1}{n}(M \cdot A ) \] เมื่อ n คือจำนวนนักเรียน (100 คน) และ M คือ matrix ขนาด \( n \times n \) และ element ทุกตัวเป็น 1 \[ \bar{X} = \frac{1}{100}\left( \begin{bmatrix} 1&1&1&\cdots\ 1&1&1&\cdots\\ 1&1&1&\cdots\\ \vdots&\vdots&\vdots\\ \end{bmatrix} \cdot \begin{bmatrix} 98&73&56\\ 35&36&12\\ 63&49&64\\ \vdots&\vdots&\vdots\\ \end{bmatrix} \right) \] \( \bar{X} \) เป็น matrix ขนาด \( 100 \times 3\)


3. คำนวณผลต่างระหว่าง \( x_i - \bar{x} \) \[ D = A - \bar{X} \] D เป็น matrix ขนาด \( 100 \times 3\)


4. คำนวณ variance และ covariance \[ COV = \frac{1}{n}(D^T \cdot D) \] Cov เป็น matrix ขนาด \( 3 \times 3\)

ผลลัพธ์คือ : \[ COV = \begin{bmatrix} 422.8611&235.6418&216.0739\\ 235.6418&229.8684&-30.8818\\ 216.0739&-30.8818&725.4211\\ \end{bmatrix} \]


รูปของตารางจะได้เป็น

Math. Eng. Art
Math. 422.8611 235.6418 216.0739
Eng. 235.6418 229.8684 -30.8818
Art 216.0739 -30.8818 725.4211

covariance matrix ที่ได้แสดงให้เราเข้าใจในการได้คะแนนดังนี้ (ดูรูปที่ 1 ประกอบ)

  • ตัวเลขในแนวเส้นทะแยงมุม (diagonal) บอกว่า คะแนนสอบในวิชาศิลปะมีการกระจายตัวมากที่สุด รองลงมาคือคณิตศาสตร์ น้อยที่สุดคือภาษาอังกฤษ
  • คะแนนสอบที่ได้ในวิชาคณิตศาสตร์มีความสัมพันธ์ในทิศทางเดียวกับอีกสองวิชา
  • คะแนนสอบที่ได้ในวิชาคณิตศาสตร์มีความสัมพันธ์กับคะแนนสอบวิชาภาษาอังกฤษมากว่าวิชาศิลปะเล็กน้อย
  • คะแนนสอบที่ได้ในวิชาภาษาอังกฤษมีความสัมพันธ์ในทิศตรงข้ามกับวิชาศิลปะ แต่ค่าของ covariance ไม่มากนัก (-30)


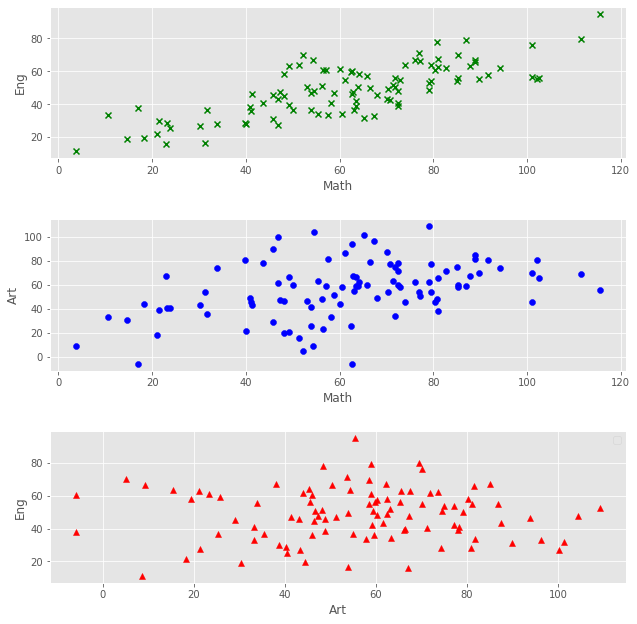รูปที่ 1 ความสัมพันธ์ระหว่างคะแนนสอบของวิชาที่สอบเมื่อนำมาจับคู่กัน


Covariance matrix กับ linear transform function

เริ่มต้นด้วยชุดข้อมูลสองมิติ  ที่ถูกสร้างขึ้นมาให้เป็น white noise หรือ white data (normal distribution มี mean = 0 และ standard deviation = 1) จะมี covariance matrix เป็น \( \begin{bmatrix} 1&0\\0&1\end{bmatrix}\) แสดงในรูปที่ 2 บน-ซ้าย แล้วลองปรับค่า element ใน covariance matrix นำมา plot เพื่อดูว่ามีการเปลี่ยนแแปลงอย่างไร

รูปที่ 2


รูปที่ 3


Covariance Matrix ผลลัพธ์
\(\begin{bmatrix} 20&0\\0&1\end{bmatrix} \) รูป 2 บน-ขวา
\(\begin{bmatrix} 1&0\\0&20\end{bmatrix} \) รูป 2 ล่าง-ซ้าย
\(\begin{bmatrix} 1&10\\10&1\end{bmatrix} \) รูป 2 ล่าง-ขวา
\(\begin{bmatrix} 20&10\\10&1\end{bmatrix} \) รูป 3 บน-ขวา
\(\begin{bmatrix} 1&10\\10&20\end{bmatrix} \) รูป 3 บน-ขวา
\(\begin{bmatrix} 20&-10\\-10&1\end{bmatrix} \) รูป 3 ล่าง-ซ้าย
\(\begin{bmatrix} 1&-10\\-10&20\end{bmatrix} \) รูป 3 ล่าง-ขวา


จะเห็นว่า ค่าของ variance และ covariance กับรูปร่างของกราฟสัมพันธ์กัน variance จะบอกขนาดของการกระจายข้อมูล (magnitude) และ covariance บอกถึงทิศทางการกระจายตัว จากความรู้เรื่อง linear transformation [4] เราจึงมอง covariance matrix ว่าทำหน้าที่เหมือนกับ transform matrix ก็ได้



Correlation

ในมุมมองทางด้านสถิติ Correlation (อาจเรียก correlation coefficient) ใช้บอกความสัมพันธ์เชิงเส้น (linear association) ระหว่าง random variable 2 ตัว (X,Y) โดยค่าของ correlation จะมีค่าระหว่าง [-1,1] หากค่าของ correlation มากกว่า 0 แสดงความสัมพันธ์ในทิศทางเดียวกัน หากน้อยกว่า 0 จะเป็นแบบผกผัน แต่หากเป็น 0 นั่นคือไม่มีความสัมพันธ์ระหว่างกัน นิยามโดย ถ้าให้ X,Y เป็น random variables \[ \begin{align*} Corr(X,Y) &= \frac{\sum_{i=1}^n{(x_i-\bar{x})(y_i-\bar{y})}} {\sqrt{\sum_{i=1}^n{(x_i-\bar{x})^2}}\sqrt{\sum_{i=1}^n{(y_i-\bar{y})^2}}} \tag{5.1} \\\\ Corr(X,Y) &= \frac{Cov(X,Y)}{\sqrt{\sigma_X^2 \sigma_Y^2}} \tag{5.2} \end{align*} \]

จาก (5.1),(5.2) อาจกล่าวได้ว่า correlation คือผลของการทำ normalization ให้กับ covariance (สังเกตุว่าจะมีการหาร covariance ด้วย norm) ดังนั้นเราจะสามารถเขียนสมการในรูปของ vector ได้ดังนี้ \[ Corr(\vec{x},\vec{y}) = \frac{(\vec{x}-\bar{x})^T \cdot (\vec{y}-\bar{y})} {\|\vec{x}-\bar{x}\| \|\vec{y}-\bar{y}\|} \tag{6} \] ถ้าให้ \( \vec{\hat{x}} = \vec{x}-\bar{x}\) และ \( \vec{\hat{y}} = \vec{y}-\bar{y}\) แล้วจะได้ \[ Corr(\vec{x},\vec{y}) = \frac{\vec{\hat{x}}^T \cdot \vec{\hat{y}}} {\|\vec{\hat{x}}\| \|\vec{\hat{y}}\|} \tag{7} \] เราทราบแล้วว่าการหาร vector ด้วยค่า norm ของ vector นั้นคือการทำให้ vector นั้นกลายเป็น unit vector ดังนั้นอาจกล่าวได้ว่า สมการ(7) ก็คือการทำ normalization ให้ column pair ของ matrix X

หากนำไปเทียบกับการหามุมระหว่าง vector สอง vector ใดๆแล้ว จะเห็นว่า สมการ (7) ก็คือสมการสำหรับหา \( cos(\theta) \) ของมุมระหว่าง \(\vec{\hat{x}},\vec{\hat{y}} \) ดังนั้นในมุมมองของ vector แล้ว correlation ก็คือการวัด collinear ระหว่าง \(\vec{\hat{x}},\vec{\hat{y}} \) นั่นเอง

กลับไปพิจารณา Matrix X และสมการ (2.3) และ (2.4) หาก \(\hat{X} \) คือ normalized from ของ X แล้ว จะได้ว่า \[ Corr(\hat{X}) = \hat{X}^T \cdot \hat{X} \tag{8} \]

กล่าวโดยสรุป ขั้นตอนสำหรับการหา correlation ใน matrix เมื่อมี data set คือ
1. สร้าง matrix โดยที่แต่ละ column vector แทนข้อมูลแต่ละ feature
2. หาค่าเฉลี่ยของแต่ละ column vector แล้วนำไปลบออกจากข้อมูลเดิม
3. ทำให้ column vector ให้เป็น unit vector ด้วยการหารด้วย norm ของแต่ละ column vector
4. สร้าง correlation matrix ด้วยสมการ (8)

เนื่องจากเป็นไปไม่ได้ที่จะทำให้เห็นภาพของการหา correlation ระหว่าง vector ที่มีมากกว่า 3 มิติ ดังนั้นจะนำเอาตัวอย่างคะแนนสอบจากตัวอย่างข้างต้นมาเพียง 2 รายการเท่านั้น ดังนี้ \[ \begin{align*} A &= \begin{bmatrix} 98&73&56\\ 35&36&12\\ 63&49&64\\ \vdots&\vdots&\vdots\\ \end{bmatrix} \\\\ \hat{A} &= \begin{bmatrix} 0.28& 0.25& 0.06 \\ -0.20& -0.24& 0.08\\ -0.56&-0.60& -0.79\\ \vdots&\vdots&\vdots\\ \end{bmatrix} \\\\ Corr(\hat{A}) &= \begin{bmatrix} 1.00&0.98&0.61 \\ 0.98&1.00&0.57 \\ 0.61&0.57&1.00 \end{bmatrix} \end{align*} \] correlation matrix ที่ได้มาตีความได้ว่าคะแนนสอบวิชาคณิตศาสตร์ (vector column ที่ 1 ใน A ) และภาษาอังกฤษ (vector column ที่ 2 ใน A ) มีความสัมพันธ์ต่อกันมากกว่า คณิตศาสตร์กับศิลปะ และทำนองเดียวกันระหว่าอภาษาอังกฤษกับศิลปะ ลองนำมาวาด vector ดูจะเห็นดังรูปที่ 4 จะเห็นได้ชัดเจนว่า vector ที่แทนคณิตศาสตร์มี collinear กับภาษาอังกฤษค่อนข้างมาก

รูปที่ 4


ความคิดเห็น

แสดงความคิดเห็น