หัวข้อ
Linearity [1]
"linear" มาจากภาษาละติน "linearis" หมายถึง เหมือนหรือสัมพันธ์กับเส้นตรง ในทางคณิตศาสตร์มอง linearity คือรูปแบบของความสัมพันธ์ระหว่างตัวแปร เมื่อนำมา plot graph แล้วจะมองได้ว่าเป็นเส้นตรง ถ้าพิจารณาสัดส่วนระหว่างตัวแปรก็จะมีแนวโน้มเข้าหาค่าคงที่ค่าหนึ่ง ตัวอย่างข้อมูลในตารางที่ 1 คือส่วนหนึ่งของข้อมูลของความสูง (ซม.) กับ น้ำหนัก (กก.) ของเด็กกลุ่มหนึ่ง กราฟแสดงความสัมพันธ์ระหว่างความสูงและน้ำหนักแสดงในรูปที่ 1 โดยใช้ข้อมูลจาก 30 คน
ตารางที่ 1 : ตัวอย่างข้อมูลแสดงความสัมพันธ์ระหว่างน้ำหนักกับความสูง
| น้ำหนัก (กก.) |
ความสูง (ซม.) |
| 50.0 | 141.9 |
| 51.0 | 148.7 |
| 52.1 | 146.6 |
| 53.1 | 153.9 |
| 54.1 | 148.7 |
| 55.2 | 151.9 |
| 56.2 | 150.1 |
| 57.2 | 150.8 |
| 58.3 | 148.9 |
| 59.3 | 150.9 |
| ... |
... |
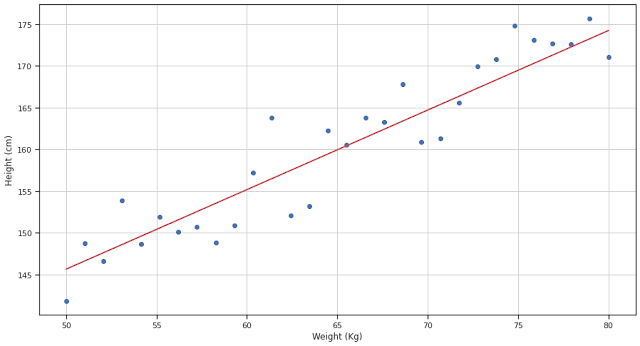 |
| รูปที่ 1 กราฟแสดงความสัมพันธ์ระหว่างความสูงกับน้ำหนัก |
ในรูปที่ 1 จุดสีน้ำเงินแทนข้อมูลที่มาจากตาราง ข้อมูลที่เก็บมาจากสภาพในธรรมชาติจริงมักไม่เรียบเหมือนกับข้อมูลที่เกิดขึ้นตามทฤษฎี แต่จะมีแนวโน้มเป็นไปตามทฤษฎี จึงสร้างเส้นตรงสีแดงเพื่อช่วยทำให้เห็นว่าความสัมพันธ์ของข้อมูลนั้นอยู่ในรูปแบบของเส้นตรง หรือมี linearity
ภาพของแนวโน้มนี้จะชัดเจนมากขึ้นเมื่อมีจำนวนข้อมูลมากขึ้น ดูได้จากรูปที่ 2 ความชัดเจนของ linearity มีมากขึ้นเมื่อใช้ข้อมูลจาก 1000 คน
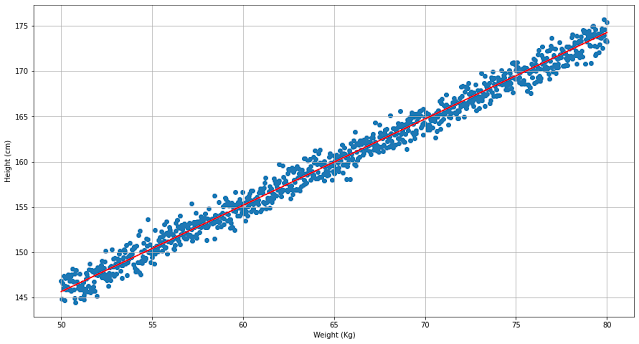 |
| รูปที่ 2 ลักษณะความสัมพันธ์แสดงให้เป็นรูปแบบเส้นตรงชัดขึ้นเมื่อจำนวนตัวอย่างเพิ่มขึ้น |
Linear equation [2]
พิจารณาตัวอย่างการทำ Green Smoothie 1 แก้ว มีส่วนผสมดังนี้
- ผักโขม 2 ถ้วยตวง
- น้ำเปล่า 2 ถ้วยตวง
- เนื้อมะม่วง 1 ถ้วยตวง
- เนื้อสัปรด 1 ถ้วยตวง
- กล้วย 1 ผล
เราอาจเขียนสูตรนี้ใหม่ในรูปแบบของสมการเชิงเส้น (linear equation) ได้ดังนี้
\[ \text{smoothie} = (2 \times \text{spinach}) + (2 \times \text{water}) + \text{mango} + \text{pineapple} + \text{banana} \tag{1.0}\]
หรือ
\[ y = 2 x_1 + 2 x_2 + x_3 + x_4 + x_5 \tag{1.1}\]
เมื่อ \( y \) แทนจำนวนแก้วของ Green smoothie
\( x_1 \) แทน spinach,
\(x_2\) แทน water,
\( x_3\) แทน mango ,
\(x_4\) แทน pineapple และ
\(x_5 \) แทน banana
สมการ (1.1) อยู่ในรูปแบบของ linear form หรือ linear equation ช่วยให้เราสามารถจัดการกับปริมาณวัตถุดิบที่จะใช้หรือปริมาณของ Green Smoothie ที่จะได้เมื่อทราบจำนวนของวัตถุดิบ เช่น ถ้าต้องการ Green Smoothie จำนวน 50 แก้ว การคำนวณหาปริมาณวัตถุดิบที่ต้องการทั้งหมดคือการด้วย 50 เข้าไปใน (1.1) ก็จะได้จำนวนวัตถุดิบแต่ละชนิดที่ต้องการ
ทำให้เราสรุปรูปแบบทั่วไปของ linear equation ได้ดังนี้
\[y = a_1x_1+a_2x_2+a_3x_3+...+a_nx_n \tag{1.3} \]
เรียก \( x_1,x_2,x_3,...,x_n\) ว่า unknown variables , \( a_1,a_2,a_3,...,a_n \) ว่า parameters หรือ coefficients
System of linear equations
เป็นการขยายความต่อจากตัวอย่างการผลิต Green Smoothie สมมุติมีโรงงาน A ผลิตและจำหน่ายสินค้า n ชนิด สินค้าแต่ละชนิดใช้วัตถุดิบ m ชนิดในปริมาณที่ต่างกัน
ถ้าให้ \( P_1 ,P_2,P_3,...,P_n\) แทนจำนวนหน่วยของสินค้าชนิดที่ 1 ,2, 3,...,n ที่จะผลิตได้
ให้ \( M_1,M_2,M_3,...,M_m \) แทนจำนวนของวัตถุดิบแต่ละชนิดที่ใช้ต้องใช้ในการผลิตสินค้า
ให้ \( a_{n,m} \) แทนจำนวนหน่วยของวัตถุดิบที่ m ใช้ในการผลิตสินค้า n
จากข้อมูลนี้นำมาเขียน linear equation ของการผลิตสินค้าชนิดต่างๆ ดังนี้
\[
\begin{align*}
P_1 &= a_{1,1}M_1 + a_{1,2}M_2+ a_{1,3}M_3+...+ a_{1,m}M_m \\
P_2 &= a_{2,1}M_1 + a_{2,2}M_2+ a_{2,3}M_3+...+ a_{2,m}M_m \\
P_3 &= a_{3,1}M_1 + a_{3,2}M_2+ a_{3,3}M_3+...+ a_{3,m}M_m \\
\vdots \\
P_n &= a_{n,1}M_1 + a_{n,2}M_2+ a_{n,3}M_3+...+ a_{n,m}M_m \\
\end{align*}
\]
collection ของ linear equations ในระบบหนึ่งลักษณะนี้เราเรียกว่า System of linear equations
สังเกตุจะพบว่า \( a_{1,1},a_{2,1},a_{3,1},...,a_{n,1} \) จะคูณด้วย \( M_1\) และ \( a_{1,2},a_{2,2},a_{3,2},...,a_{n,2} \) จะคูณด้วย \( M_2\) แบบนี้ไปเรื่อยๆ จนถึง \( a_{1,m},a_{2,m},a_{3,m},...,a_{n,m} \) จะคูณด้วย \( M_m \) นั่นคือ system of linear equations อาจถูกเขียนในแบบของ vector - scalar multiplicationได้ดังนี้
\[
\begin{bmatrix}P_1\\P_2\\P_3\\\vdots\\P_n\end{bmatrix} =
M_1 \cdot \begin{bmatrix}a_{1,1}\\a_{2,1}\\a_{3,1}\\\vdots\\a_{n,1} \end{bmatrix} +
M_2 \cdot \begin{bmatrix}a_{1,2}\\a_{2,2}\\a_{3,2}\\\vdots\\a_{n,2} \end{bmatrix} +
M_3 \cdot \begin{bmatrix}a_{1,3}\\a_{2,3}\\a_{3,3}\\\vdots\\a_{n,3} \end{bmatrix} +
\cdots +
M_m \cdot \begin{bmatrix}a_{1,m}\\a_{2,m}\\a_{3,m}\\\vdots\\a_{n,m} \end{bmatrix} \tag{2.1}
\]
หรือ แปลงให้อยู่ในรูปแบบของ matrix dot operation ( มองว่า vector เป็น column matrix)
\[
\begin{align*}
\begin{bmatrix}P_1\\P_2\\P_3\\\vdots\\P_n\end{bmatrix} &=
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,m} \\
a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,m} \\
a_{3,1} & a_{3,2} & a_{3,3} & \cdots & a_{3,m}\\
\vdots & \vdots & \vdots & \cdots & \vdots \\
a_{n,1} & a_{n,2} & a_{n,3} & \cdots & a_{n,m}
\end{bmatrix}
\cdot
\begin{bmatrix}M_1\\M_2\\M_3\\\vdots\\M_m \end{bmatrix} \\\\
\vec{P} &= A \cdot \vec{M} \tag{2.2}
\end{align*}
\]
สมการ (2.2) อาจถูกเรียกว่า ฟังก์ชั่นเป้าหมาย (objective function)
Linear function [3,4]
สมมุติว่าทราบความสัมพันธ์บางอย่างของ unknown variable 3 ตัว ในรูปแบบ \(8a -4b +10c = 20 \) นั่นคือ
\[ \begin{align*} 4b &=8a +10c -20 \\ b &=2a +\frac{5}{2}c -5 \end{align*} \]
หมายความว่าหากเราทราบค่าของ a และ c แล้ว ก็จะสามารถหาค่าของ b ได้ หรือหากทราบค่าของสองตัวแปรใดๆ จะหาค่าของตัวแปรที่เหลือได้ ถ้ามองในมุม function a,c คือ input และ b คือ output ความสัมพันธ์ในรูปแบบของ function เขียนได้ดังนี้
\[ f(a,c) = 2a + \frac{5}{2}c - 5\]
ทำนองเดียวกัน linear equation (1.3) ก็ถูกมองในรูปแบบของ function ได้โดยทุก unknown variables \( x_n \) คือ input ของ function สมการ (1.3) เขียนใหม่ได้เป็น
\[
f(x_1,x_2,x_3,...,x_n) = a_1x_1 + a_2x_2+a_3x_3 +...+a_nx_n \tag{3.1}
\]
เรียกว่า (3.1) ว่า linear function เมื่อนำแนวคิดเรื่อง vector dot product [5] มาใช้กับสมการ (3.1) จะเขียนใหม่ได้เป็น
\[
\begin{align*}
f(x_1,x_2,x_3,...,x_n) &= \begin{bmatrix}a_1\\a_2\\a_3\\ \vdots \\a_n \end{bmatrix} \cdot
\begin{bmatrix}x_1\\x_2\\x_3\\ \vdots \\x_n \end{bmatrix} \\\\
f(\vec{x}) &= \vec{a} \cdot \vec{x} \tag{3.2}
\end{align*}
\]
เราทราบว่า \( f(\vec{x}) \in \Re \) และ \( \vec{a} \cdot \vec{x} \in \Re^n \) จึงสรุปได้ว่า linear function คือ function ที่ map จาก set ของ n-vectors ไปสู่ set ของ real number \( f: \Re^n \rightarrow \Re \)
Linear mapping [6]
คำว่า "mapping" คือ กฎที่ใช้ระบุการจับคู่สมาชิกใดๆของ set หนึ่งไปยังอีก set หนึ่งในลักษณะแบบ many to one ซึ่งเป็นความหมายเดียวกันกับ "function" [7] เพียงแต่เมื่อกล่าวในบริบทของ linear mapping จะใช้กับการโยงระหว่าง vector space แทน set
ถ้า T คือ function หรือ mapping ระหว่าง vector space V ไปยัง vector space W เขียนแทนด้วย \( T : V \rightarrow W\) สำหรับ \( \vec{u},\vec{v} \in V \) แล้ว T ต้องสอดคล้องกับคุณสมบัติสองข้อคือ
- \( T(\vec{v}+\vec{u}) = T(\vec{v}) + T(\vec{u})\)
- \( T(a\vec{v}) = aT(\vec{v})\)
ถ้ามี \( \vec{v} = \begin{bmatrix}v_1\\v_2\\\vdots\\v_n \end{bmatrix} \) จะสามารถเขียน \(\vec{v} \) ในรูปแบบของ span คือ \( v_1 \cdot \vec{e_1} + v_2 \cdot \vec{e_2} + ... + v_n \cdot \vec{e_n} \) เมื่อ \( \vec{e_1},\vec{e_2},\vec{e_3},...,\vec{e_n} \) คือ basis vectors ของแต่ละแกนบน plane เช่น \( \begin{bmatrix} 3 \\ 7 \end{bmatrix} = 3 \begin{bmatrix} 1 \\ 0\end{bmatrix} + 7 \begin{bmatrix} 0 \\1\end{bmatrix}\)
นั่นคือ
\[
\begin{align*}
T(\vec{v}) &= T(v_1 \cdot \vec{e_1} + v_2 \cdot \vec{e_2} + ... + v_n \cdot \vec{e_n}) \\
&= T(v_1 \cdot \vec{e_1}) + T(v_2 \cdot \vec{e_2}) + ... + T(v_n \cdot \vec{e_n}) \\
&= v_1 \cdot T( \vec{e_1}) + v_2 \cdot T( \vec{e_2}) + ... + v_n \cdot T(\vec{e_n}) \\\\
\therefore T(\vec{v}) &= v_1 \cdot T( \vec{e_1}) + v_2 \cdot T( \vec{e_2}) + ... + v_n \cdot T(\vec{e_n}) \tag{4.1} \\\\
\end{align*}
\]
พิจารณาสมการ \((4.1) \) จะเห็นว่าสามารถมองในรูปแบบของ matrix-vector multiplication ได้ คือ
\[\begin{align*}
T(\vec{v}) &= \begin{bmatrix} T( \vec{e_1}) & T( \vec{e_2}) & ... T( \vec{e_n})\end{bmatrix} \cdot
\begin{bmatrix} v_1\\v_2\\ \vdots \\ v_n \end{bmatrix} \\\\
\therefore T(\vec{v}) &= A\cdot\vec{v} \tag{4.2} \\
\end{align*}
\]
เรียก A ใน (4.2) ว่า Transform Matrix
ตัวอย่าง ต้องการหา vector ที่ตั้งฉากกับ \(\vec{u}= \begin{bmatrix} 2 \\3\end{bmatrix} \) ในทิศทางตามเข็มนาฬิกา
จากกำหนดให้ \(\vec{u} \in \Re^2 \) ทำให้ทราบว่า \(\begin{bmatrix} 1 \\0\end{bmatrix},\begin{bmatrix} 0 \\ 1\end{bmatrix} \) คือ basis ของ dimension ที่ 1 และ 2 ตามลำดับ
พิจารณา \(\begin{bmatrix} 1 \\0\end{bmatrix} \) vector ที่ตั้งฉากกันในทิศตามเข็มนาฬิกาคือ \(\begin{bmatrix} 0 \\-1\end{bmatrix} \)
พิจารณา \(\begin{bmatrix} 0 \\1\end{bmatrix} \) vector ที่ตั้งฉากกันในทิศตามเข็มนาฬิกาคือ \(\begin{bmatrix} 1 \\ 0\end{bmatrix} \)
นำไปแทนค่าตาม \( (4.1) \) target vector ที่ได้ก็คือ \(2 \times \begin{bmatrix} 0 \\-1\end{bmatrix}+ 3 \times \begin{bmatrix} 1 \\ 0\end{bmatrix} = \begin{bmatrix} 3 \\ -2\end{bmatrix} \)
ตัวอย่าง ถ้ามี \( \vec{u} = \begin{bmatrix} 3\\6\end{bmatrix} \) และ \( A = \begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix}\) จะสามารถสร้าง \( \vec{v} \) ที่ได้จาก การทำ linear mapping ดังนี้
\[
\begin{align*}
\vec{v} &= A \cdot \vec{u} \\\\
\vec{v} &= \begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix} \cdot \begin{bmatrix} 3\\6\end{bmatrix} \\\\
\vec{v} &= \begin{bmatrix} 6\\-3\end{bmatrix}
\end{align*}
\]
ในกรณีนี้ \(T:\vec{u}\rightarrow \vec{v} \) คือ \( T(\vec{u}) = A \cdot \vec{u} \) นำ \( \vec{u},\vec{v} \) ไปวาดลงบน plate จะเห็นว่าตั้งฉากกัน นั่นคือ T ในตัวอย่างนี้คือการ map \(\vec{u} \) ไปหา orthogonal vector
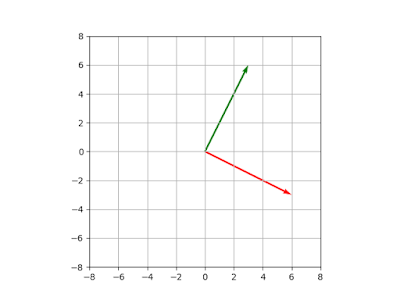 |
| รูปที่ 3 |
ตัวอย่าง จากตัวอย่างก่อนหน้า จงพิสูจน์ว่า \( T:u \rightarrow v \) สอดคล้อง
กับคุณสมบัติของ linear mapping หรือไม่
พิสูจน์ว่า \( A \cdot (\vec{u}+ \vec{v}) = A \cdot \vec{u} + A \cdot \vec{v} \) สมมุติให้ \( \vec{v} = \begin{bmatrix}2\\3\end{bmatrix} \)
\[
\begin{align*}
A \cdot (\vec{u}+\vec{v}) &= \begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix} \cdot (\begin{bmatrix} 3\\6\end{bmatrix} +\begin{bmatrix}2\\3\end{bmatrix} ) \\
&= \begin{bmatrix}9\\-5\end{bmatrix} \tag{4.3}\\\\
A \cdot\vec{u}+ A\cdot\vec{v} &= \begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix} \cdot \begin{bmatrix} 3\\6\end{bmatrix} +
\begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix} \cdot \begin{bmatrix}2\\3\end{bmatrix}\\
&= \begin{bmatrix}9\\-5\end{bmatrix} \tag{4.4}\\\\
\end{align*}
\]
(4.3) = (4.4) สอดคล้องกับคุณสมบัติข้อแรก
พิสูจน์ว่า \( A \cdot (a \times \vec{u}) = a \times (A \cdot \vec{u}) \) สมมุติให้ \( a =3 \)
\[
\begin{align*}
A \cdot (3 \times \vec{u}) &= \begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix} \cdot \begin{bmatrix} 9\\18\end{bmatrix} \\
&= \begin{bmatrix}18\\-9\end{bmatrix} \tag{4.5}\\\\
3\times (A \cdot\vec{u}) &= 3 \times (\begin{bmatrix} 0 & 1 \\ -1&0 \end{bmatrix} \cdot \begin{bmatrix} 3\\6\end{bmatrix} )\\
&= \begin{bmatrix}18\\-9\end{bmatrix} \tag{4.6}\\\\
\end{align*}
\]
(4.5) = (4.6) สอดคล้องกับคุณสมบัติข้อแรก
ตัวอย่าง Transform matrix linear mappings
การทำ linear mapping ด้วย matrix transform จะพบได้บ่อยในงานด้าน image processing , computer vision และ neural network ตัวอย่าง transform matrix แสดงในตารางที่ 2 [8] เช่น
ตารางที่ 2 ตัวอย่าง transform matrix สำหรับ linear mapping ในงาน computer graphic
| Transformation | Matrix | Note |
|---|
| Scaling | \(
\begin{bmatrix}
s_x & 0 & 0\\
0 & s_y & 0 \\
0 & 0 & 1 \\
\end{bmatrix}\) | |
| Rotation | \( \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \\ \end{bmatrix} \) | |
| Shearing | \( \begin{bmatrix} 1 & s_h & 0 \\ s_v & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\) | |
ตัวอย่างการทำ linear mapping ด้วย rotation matrix ด้วยมุม \( 45 ^\circ \)ทำให้เกิดการเปลี่ยนแปลงขึ้นดังรูปที่ 4 และ 5 input vectors แทนด้วยสีแดง output vectors แทนด้วยสีฟ้า จะสังเกตุเส้นประซึ่งแสดงให้เห็นการเปลี่ยนตำแหน่งของของรูปสี่เหลี่ยมมีการหมุนหรือการย้ายตำแหน่ง โดยที่สัดส่วนไม่ได้มีการเปลี่ยน
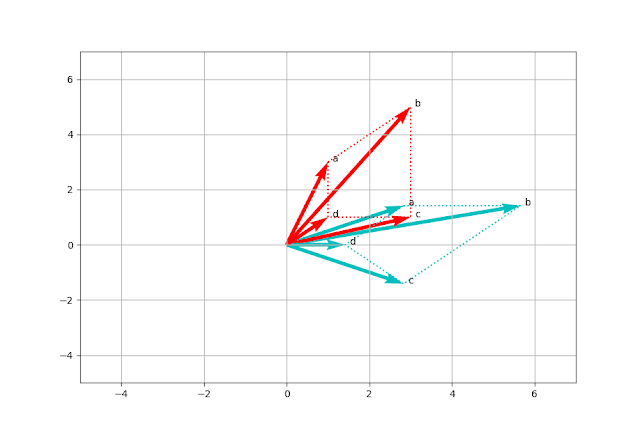 |
| รูปที่ 4 ผลของการใช้ rotation matrix |
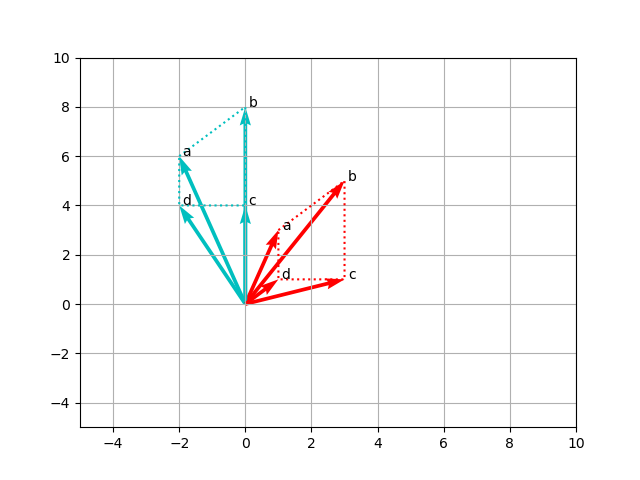 |
| รูปที่ 5 ผลของการใช้ translation matrix |
การใช้ linear mapping ในการเปลี่ยน color space ของภาพ เพื่อช่วยในการวิเคราะห์ภาพ จาก Red Green Blue (RGB) color space [11] ไปยัง Luminance, Chrominance (YCbCr) [12] โดยใช้สมการ
\[
\begin{align*}
A \cdot \text{RGB} &= \text{YCbCr}\\\\
\begin{pmatrix} 0.299&0.587&0.114 & 0 \\ -0.169&-0.331&0.5&128 \\ 0.5 & -0.419 &-0.081 &128 \end{pmatrix} \cdot \begin{pmatrix}R\\G\\B \end{pmatrix} &= \begin{pmatrix}Y\\Cb\\Cr \end{pmatrix}
\end{align*}
\]
 |
| รูปที่ 6 ภาพที่แสดงด้วย YCrCb (บน) และ RGB (ล่าง) แยกตาม channel |
จากรูปที่ 6 ภาพที่ใช้ RGB colorspace (3 ภาพล่าง) เมื่อแยกออกมาแสดงเป็นแต่ละ channel (Red, Gree, Blue) แล้ว จะเห็นว่ามีความแตกต่างน้อย ในขณะที่ภาพที่ใช้ YCbCr colorspace (3 ภาพบน) จะแสดงความแตกต่างกันในแต่ละ channel (Y,Cr,Cb) ได้ชัดเจนกว่า
Translation
Translation เป็น linear mapping แบบหนึ่ง ที่อยู่ในรูปแบบ \( T : R^n \rightarrow R^n \) โดยที่ \[ T(\vec{x}) = \vec{x} + \vec{b} \tag{5.0}\] เมื่อ \( \vec{b} \) เป็น vector ที่ไม่เปลี่ยนแปลง (fixed vector) ตัวอย่างแสดงในรูปที่ 7 set ของ vector เดิมแทนด้วยสีแดง set ของ vector ที่ถูก translate แทนด้วยสีน้ำเงิน
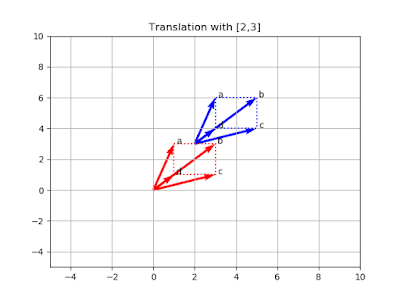 |
| รูปที่ 7 แสดงการ translate ด้วย \( \vec{b}=\begin{bmatrix} 2\\3 \end{bmatrix}\) |
Affine mapping [9,10]
Affine mapping หรือ affine function คือ function ที่มีกิจกรรมสองอย่างคือ linear mapping และ translation รูปแบบทั่วไปคือ
\[ A(\vec{x}) = M \cdot \vec{x} +\vec{b} \tag{6.0}\]
เมื่อ M คือ linear transform matrix (linear mapping matrix) และ \(\vec{b}\) คือ translation vector
โดยนิยามแล้ว ทุก linear function ถือว่าเป็น affine function แต่ไม่ทุก affine function จะเป็น linear function พิสูจน์ได้จาก ถ้ากำหนดให้ \[ \begin{align*}A(\vec{u}) &= M \cdot \vec{u} + \vec{b}\\\\ A(\vec{v}) &= M \cdot \vec{v}+\vec{b} \end{align*}\]
แล้วจะได้
\[ A(\vec{u} + \vec{v}) = M \cdot (\vec{u} + \vec{v})+ \vec{b} \]
ในขณะที่
\[ \begin{align*} A(\vec{u}) + A(\vec{v}) &= M \cdot \vec{u} + \vec{b} + M \cdot \vec{v} + \vec{b} \\ &= M \cdot (\vec{u} \cdot \vec{v}) + 2\vec{b} \end{align*} \]
จะเห็นได้ว่า \( A(\vec{u} + \vec{v}) \neq A(\vec{u}) + A(\vec{v})\) ในกรณีของ affine function
ตัวอย่างการสร้าง affine function ที่ประกอบด้วย linear function คือการทำ shearing ด้วย \(\begin{bmatrix} 1 & 0.4 \\ 0 & 1 \end{bmatrix}\) (ดูตารางที่ 2) และ translation ด้วย \( \begin{bmatrix} 3\\3\end{bmatrix}\) ของลุ่ม vector \( \begin{bmatrix}1\\3\end{bmatrix},
\begin{bmatrix}3\\3\end{bmatrix},
\begin{bmatrix}3\\1\end{bmatrix},
\begin{bmatrix}1\\1\end{bmatrix}\)
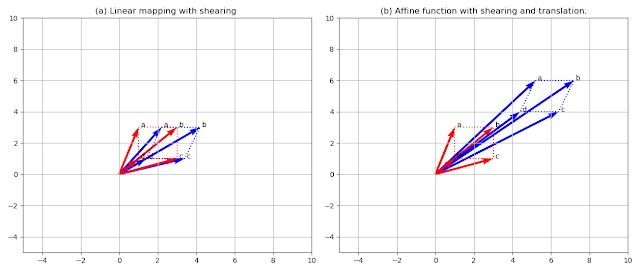 |
| รูปที่ 8 linear mapping ด้วย shearing (ซ้าย) affine mapping ด้วย shearging และ translation (ขวา) |
\[
\begin{align*}
A(\begin{bmatrix}1\\3\end{bmatrix}) &= \begin{bmatrix} 1 & 0.4 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix}1\\3\end{bmatrix} + \begin{bmatrix} 3\\3\end{bmatrix} \\\\
A(\begin{bmatrix}1\\3\end{bmatrix}) &= \begin{bmatrix} 5.2\\6\end{bmatrix}
\end{align*}
\]
ด้วยวิธีการของ augmatation เราสามารถเขียนสมการนี้ใหม่ได้ด้วย
\[
\begin{align*}
A(\begin{bmatrix}1\\3\end{bmatrix}) = \begin{bmatrix} 1 & 0.4 & 3 \\ 0 & 1 & 3 \end{bmatrix} \cdot \begin{bmatrix}1 \\3 \\1 \end{bmatrix} \\
\end{align*}
\]
vector ที่เหลือก็สามารถจัดการด้วยวิธีการเดียวกันได้ ผลที่ได้ดูจากรูปที่ 8
Affine function ใน perceptron
perceptron เป็นพื้นฐานของ neural network ใน perceptron มี 2 functions ทำงานร่วมกัน คือ accumulation function และ activation function [13] ในส่วน accumulation function คือ
\[ g(x) = \sum_{i=1}^{n}w_i x_i + b\]
ถ้าให้ x ,b เป็น vector และ w เป็น matrix เราก็สามารถเขียนในรูปแบบของ operation ระหว่าง matrix กับ vector ได้
\[ g(\vec{x}) = W \cdot \vec{x} + \vec{b} \]
จะเห็นว่า \( g(\vec{x}) \) ก็คือ affine function นั่นคือภายใน neural network (ไม่นับ learning algorithm ) คือ affine function กับ activation function
Projection transformation
Projection เหมือนกับการเกิดเงาของคนบนกำแพง หากเทียบคนกับ vector แล้วกำแพงเทียบกับ axis หรือ plane เงาของคนบนกำแพงหรือพื้นก็คือ projection vector ของคน
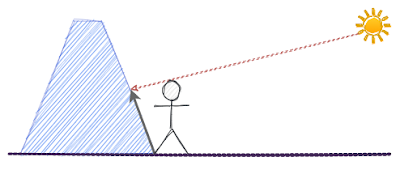 |
| รูปที่ 9 เงาของคนบนกำแพงเทียบได้กับ projection vector |
ใน 2 D space , ถ้า projection ของ \( \vec{x} = \begin{bmatrix} x\\y \end{bmatrix} \) บน X - axis คือ \( \begin{bmatrix} x^\prime\\ y^\prime \end{bmatrix}\) แล้ว จะได้
\[
\begin{align*} x^\prime &= x + 0y \\ y^\prime &= 0 + 0y
\end{align*}
\]
หรืออาจเขียนให้อยู่ในรูปของ linear transformation คือ
\[
\begin{align*}
\begin{bmatrix}x^\prime\\ y^\prime\end{bmatrix} &= \begin{bmatrix}1 & 0 \\0 & 0 \end{bmatrix} \cdot \begin{bmatrix}x \\ y \end{bmatrix}
\end{align*}
\]
ทำนองเดียวกัน projection vector บน Y-axis หาได้จาก
\[
\begin{align*}
\begin{bmatrix} x^\prime\\ y^\prime \end{bmatrix} &= \begin{bmatrix}0 & 0 \\0 & 1 \end{bmatrix} \cdot \begin{bmatrix}x \\ y \end{bmatrix}
\end{align*}
\]
สรุปคือ transform matrix สำหรับ \(\vec{x} = \begin{bmatrix} x \\ y \end{bmatrix} \) บน X-axis คือ \(\begin{bmatrix}1 & 0 \\0 & 0 \end{bmatrix} \) และบน Y-axis คือ \(\begin{bmatrix}0 & 0 \\0 & 1 \end{bmatrix} \)
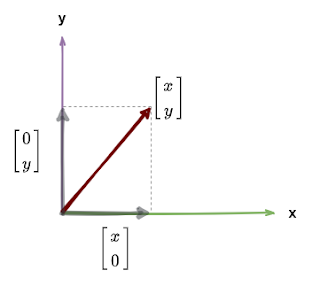 |
| รูปที่ 10 projection บน x-axis หรือ y-axis |
ใน 3 D space หรือมากกว่า หลักการยังคงเหมือนเดิมแต่ projection vector จะเป็น vector บน plane ไม่ใช่บน axis
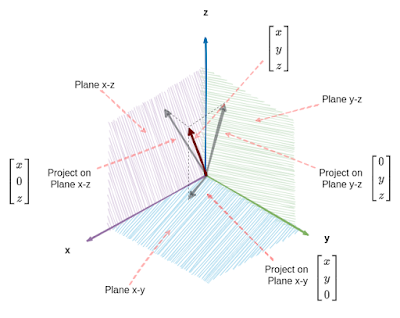 |
| รูปที่ 11 projection vector ที่มี dimension มากกว่า 2 จะอยู่บน plane |
ถ้ามี \( \begin{bmatrix} x\\y\\z \end{bmatrix}\) projection ที่เกิดขึ้นจะอยู่บน plane ได้ทั้ง plane คือ x-y, x-z, หรือ y-z
บน plane x-y
\[
\begin{align*}
x^\prime &= x + 0y + 0z \\
y^\prime &= 0x + y + 0z \\
z^\prime &= 0x + 0y + 0z \\\\
\begin{bmatrix} x^\prime\\y^\prime\\z^\prime \end{bmatrix} &=
\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}
\cdot
\begin{bmatrix} x\\y\\z \end{bmatrix}
\end{align*}
\]
บน plane x-z
\[
\begin{align*}
x^\prime &= x + 0y + 0z \\
y^\prime &= 0x + 0y + 0z \\
z^\prime &= 0x + 0y + z \\\\
\begin{bmatrix} x^\prime\\y^\prime\\z^\prime \end{bmatrix} &=
\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\cdot
\begin{bmatrix} x\\y\\z \end{bmatrix}
\end{align*}
\]
บน plane y-z
\[
\begin{align*}
x^\prime &= 0x + 0y + 0z \\
y^\prime &= 0x + y + 0z \\
z^\prime &= 0x + 0y + z \\\\
\begin{bmatrix} x^\prime\\y^\prime\\z^\prime \end{bmatrix} &=
\begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\cdot
\begin{bmatrix} x\\y\\z \end{bmatrix}
\end{align*}
\]
กลับไปเทียบกับเรื่องของเงา เงาของคนเป็นภาพที่เกิดบนพื้นผิว 2 มิติ และหากเราใช้การสังเกตุเงาแทนการสังเกตุที่ตัวคน กริยาที่สังเกตุได้จากเงาจะสอดคล้องกับกริยาที่คนกระทำ นั้นคือเราสามารถเข้าใจสิ่งที่เกิดขึ้นจากภาพ 2 มิติแทนการสังเกตุภาพที่เกิดใน 3 มิติได้ การทำ projection ไปบน plane หรือ a-xis ก็คล้ายกัน projection ที่เกิดขึ้นจะมีมิติลดลงจาก vector เดิมแต่เราก็ยังสามารถนำมาใช้งานและผลที่ได้มาก็ยังสอดคล้องกับผลที่จะเกิดขึ้นกับ vector จริงอยู่
Reflection across a line
เมื่อแสงอาทิตย์ส่องมายังพื้นผิวที่สะท้อนแสงได้ก็จะเกิดการสะท้อนของแสงขึ้น (reflection) แสงที่ตกกระทบกับแสงสะท้อนจะทำมุมกับเส้นตรงที่ตั้งฉากกับพื้นผิวด้วยมุมที่เท่ากัน
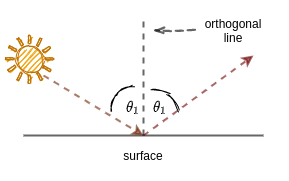 |
| รูปที่ 12 |
ในทาง linear transform หากต้องการหา reflection vector ด้วยการใช้ matrix transform เราจำเป็นต้องหา matrix นั้นก่อน
กำหนดให้เส้นตรง\(L_1\) บน 2D space แทนด้วยสมการ \( y = mx\) และมี \(\vec{a} \) ที่ไม่อยู่บนเส้นตรง \( L_1 \) (ดูรูปที่ 13) เทียบกับรูปที่ 12 แล้ว \( L_1\) คือ orthogonal line \( \vec{a} \) คือ แสงอาทิตย์ที่ตกลงมา (แต่เราจะพิจารณาในทิศทางตรงข้าม) การจะหา reflection ของ \( \vec{a} \) รอบ \(L_1\) จำเป็นต้องหาส่วนที่หายไปก่อน คือ สิ่งที่เทียบได้กับพื้นผิวสะท้อนแสง
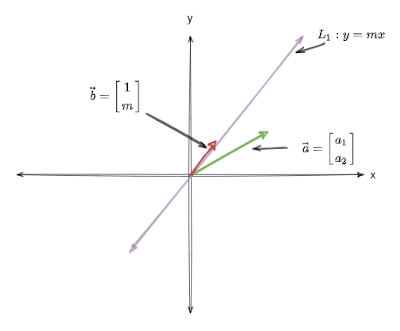 |
| รูปที่ 13 |
เราทราบว่า เส้นตรงสองเส้นที่ตั้งฉากกัน เมื่อเอาความชันมาคูณกันจะได้ผลลัพธ์เป็น -1 นั่นคือ \[ L_2 = -\frac{1}{m}x\] คือเส้นตรงที่ตั้งฉากกับ \(L_1\) (รูปที่ 14)
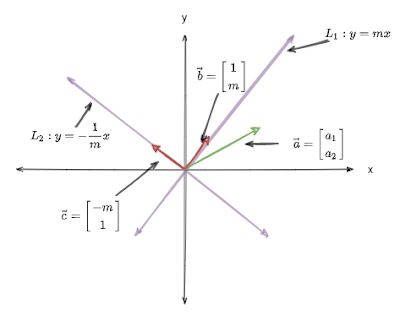 |
| รูปที่ 14 |
กำหนดให้ M เป็น Transform matrix ที่ใช้คำนวณหา reflection vector \(\vec{r}\) ในระบบ 2D space แล้ว จะได้ว่า
\[ M \cdot \vec{a} = \vec{r} \]
พิจารณาเส้นตรง \( L_1 \), เมื่อ x =1 แล้ว y = m นั่นคือ \( \vec{b} = \begin{bmatrix} 1\\m \end{bmatrix}\) จะต้องอยู่บนเส้นตรง \(L_1\) และ reflection vector ของ \(\vec{b} \) ก็ต้องเป็น \(\vec{b} \) (นึกถึงการฉายไฟฉายใส่กระจกโดยที่แนวของไฟฉายตั้งฉากกับกระจก) ดังนั้น \[
\begin{align*}
M \cdot \vec{b} &= \vec{b} \\
M \cdot \begin{bmatrix}1\\m\end{bmatrix} &= \begin{bmatrix}1\\m\end{bmatrix} \tag{9.0} \\
\end{align*}
\]
พิจารณาเส้นตรง \( L_2 \), เมื่อ x = -m แล้ว y = 1 นั้นคือ \( \vec{c} = \begin{bmatrix} m\\-1 \end{bmatrix}\) จะอยู่บนเส้นตรง \( L_2 \) ทำให้เราทราบต่อไปว่า \( \vec{r}_c = \begin{bmatrix}m\\-1\end{bmatrix}\) คือ reflection vector ของ \( \vec{c} \) (ดูรูป 15)
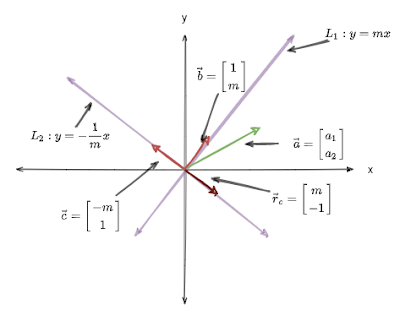 |
| รูปที่ 15 |
นั่นคือ \[
\begin{align*}
M \cdot \vec{c} &= \vec{r}_c \\\\
M \cdot \begin{bmatrix} -m\\1 \end{bmatrix} &= \begin{bmatrix}m\\-1\end{bmatrix} \tag{9.1}
\end{align*}
\]
จาก (9.0) และ (9.1) นำไปสู่ข้อสรุป
\[
M \cdot \begin{bmatrix}1 & -m \\m & 1 \end{bmatrix} = \begin{bmatrix}1 & m \\m & -1\end{bmatrix} \tag{9.2}
\]
แก้สมการ (9.2) เพื่อหา transform matrix M
\[\begin{align*}
M \cdot \begin{bmatrix}1 & -m \\m & 1 \end{bmatrix} &= \begin{bmatrix}1 & m \\m & -1\end{bmatrix} \\\\
M \cdot \begin{bmatrix}1 & -m \\m & 1 \end{bmatrix} \cdot \begin{bmatrix}1 & -m \\m & 1 \end{bmatrix}^{-1}
&= \begin{bmatrix}1 & m \\m & -1\end{bmatrix} \cdot \begin{bmatrix}1 & -m \\m & 1 \end{bmatrix}^{-1} \\\\
M &= \begin{bmatrix}1 & m \\m & -1\end{bmatrix} \cdot \frac{1}{1+m^2}\begin{bmatrix}1 & m \\-m & 1 \end{bmatrix} \\\\
M &= \frac{1}{1+m^2} \cdot \begin{bmatrix}1 & m \\m & -1\end{bmatrix} \cdot \begin{bmatrix}1 & m \\-m & 1 \end{bmatrix} \\\\
M &= \frac{1}{1+m^2} \cdot \begin{bmatrix}1-m^2 & 2m \\2m & m^2-1\end{bmatrix} \tag{9.3}
\end{align*}
\]
ประเด็นต่อเนื่องจาก (9.3) เมื่อ
- เส้นตรง \( L_1 \) ขนานกับ x - axis ความชันของเส้นตรง (m) = 0, M = \( \begin{bmatrix}1 & 0 \\0 & 1\end{bmatrix} \)
- เส้นตรง \( L_1 \) ทำมุม \( 45^\circ \) กับ x - axis ความชันของเส้นตรง (m) = 1, M = \( \begin{bmatrix}0 & 1 \\1 & 0\end{bmatrix} \)
- เส้นตรง \( L_1 \) ทำมุม \( 90^\circ \) กับ x - axis ความชันของเส้นตรง (m) = \( \infty \), M = \( \begin{bmatrix}-1 & 0 \\0 & 1\end{bmatrix} \)
















ความคิดเห็น
แสดงความคิดเห็น