"Orthogomal matrix" คือ matrix ที่มีคุณสมบัติดังนี้
1. เป็น sqaure matrix
2. column vectors ตั้งฉากต่อกัน
3. row vectors ตั้งฉากต่อกัน
4. inverse matrix คือ transpose matrix
ถ้ากำหนดให้ \[ V =
\begin{bmatrix} 0.91 & -0.21 & 0.36\\
0.31& -0.22& -0.92\\
0.27& 0.95& -0.14
\end{bmatrix}
\]
ได้ column vectors ของ V ดังนี้
\[
\vec{v}_1 = \begin{bmatrix} 0.91 \\0.31\\0.27\end{bmatrix},
\vec{v}_2 = \begin{bmatrix}-0.21\\-0.22\\ 0.95\end{bmatrix},
\vec{v}_3 =\begin{bmatrix}0.36\\-0.92\\-0.14 \end{bmatrix}
\]
นำมาค่า dot product ของ column vectors ทีละคู่
\[
\begin{align*}
\vec{v}_1 \cdot \vec{v}_2 \approx 0.002 \\
\vec{v}_1 \cdot \vec{v}_3 \approx 0.004 \\
\vec{v}_2 \cdot \vec{v}_3 \approx -0.006
\end{align*}
\]
จะเห็นว่ามีค่าใกล้เคียงศูนย์ (ไม่เท่ากับศูนย์ เนื่องจากค่าตัวเลขที่ยกมาเป็นตัวอย่างเกิดจากการประมาณค่า) ดูเหมือนว่า vectors เหล่านี้ตั้งฉากต่อกัน (orthogonal vectors)
เมื่อนำเอา column vectors มาหา norm (magnitude, length) พบว่า
\[ \begin{align*}
\|\vec{v}_1 \| \approx 0.99 \\
\|\vec{v}_2 \|\approx 0.99 \\
\|\vec{v}_3\| \approx 0.99 \end{align*}
\]
หา inverse และ transpose ของ V
\[
\begin{align*}
V^{-1} &= \begin{bmatrix}
0.91 & 0.31 & 0.27\\
-0.21 & -0.23 & 0.95\\
0.36 & -0.93 & -0.14
\end{bmatrix} \\\\
V^T &= \begin{bmatrix}
0.91 & 0.31 & 0.27\\
-0.21 & -0.23 & 0.95\\
0.36 & -0.93 & -0.14
\end{bmatrix}
\end{align*}
\]
\[\therefore V^T = V^{-1} \tag{1}\]
แสดงว่า
\[
V \cdot V^T = V \cdot V^{-1} = I \tag{2}
\]
จากคุณสมบัติที่แสดงมา สรุปได้ matrix V เป็น orthogonal matrix นอกจากนี้ norm ของ column vectors หรือ row vectors มีค่าเป็น 1.0 (ใกล้ 1.0 มาก) ในกรณีนี้ จะเรียก matrix V ว่าเป็น "Orthonormal matrix"
ตัวอย่างหนึ่งของการใช้ประโยชน์ของ orthogonal matrix คือ rotation matrix
\[
R = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta\end{bmatrix}
\]
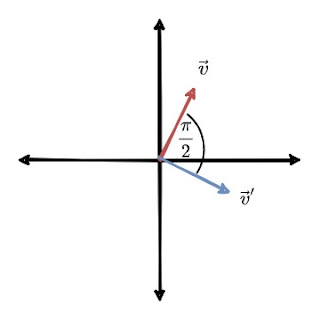
โดย \( \theta \) คือมุมที่ต้องการให้ vector หมุนไป (ตามเข็มนาฬิกา) เช่น ต้องการให้ \( \vec{v} = \begin{bmatrix} 1 \\ 2\end{bmatrix} \) หมุนไป \(\frac{\pi}{2} \) radians
\[
\begin{align*}
\vec{v}^\prime &= \begin{bmatrix} cos(\frac{\pi}{2}) & sin(\frac{\pi}{2}) \\ -sin(\frac{\pi}{2}) & cos(\frac{\pi}{2}) \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2\end{bmatrix} \\ \\
\vec{v}^\prime &= \begin{bmatrix} 2 \\ -1 \end{bmatrix}
\end{align*}
\]
เอกสารอ้างอิง
[1] https://en.wikipedia.org/wiki/Orthogonal_matrix

ความคิดเห็น
แสดงความคิดเห็น