Genetic Algorithm ตอนที่ 4 : Curve fitting

จาก ตอนที่ 3  เป็นตัวอย่างการแก้ปัญหา toy problem ในตัวอย่างนี้จะแสดงอีกตัวอย่างหนึ่งของการนำเอา GA มาใช้กับข้อมูลจริง

เตรียมและวิเคราะห์ข้อมูล

เพื่อให้เข้ากับสถานการณ์ ข้อมูลที่จะนำมาใช้เป็นข้อมูลจากสถานการณ์การแพร่ระบาดของ Covid -19 [1][3] โดยนำเอามาเฉพาะข้อมูลจำนวนผู้ติดเชื้อสะสมช่วงเวลาตั้งแต่ 1 ก.พ.  ถึง 31 พ.ค.  2020 ของประเทศไทยมาใช้ (download csv file) (เพราะแต่ละประเทศมีลักษณะของการระบาดต่างกัน)

ข้อมูลจำนวนผู้ติดเชื้อรายวัน แสดงในรูปตารางข้อมูล

date	cases
1	0
2	0
3	0
4	6
5	6
...	...
119	3057
120	3058
121	3062

รูปที่ 1 จำนวนผู้ติดเชื้อสะสมของไทย ตั้งแต่ 1 ก.พ. ถึง 31 พ.ค. 

เมื่อนำข้อมูลมา plot ก็ได้รูปร่างของเส้นกราฟออกมาเป็น S-shape หรือ Sigmoid [2] ตามรูปที่ 1  ชัดเจน ทำให้เราสามารถนำตัวแบบหรือสมการที่ใช้ในการประมาณจำนวนประชากร ณ เวลาใดๆ มาใช้กับการหาสมการเชิงเส้นที่ใช้อธิบายรูปของการระบาดในไทยได้ [4] 

\[ P(t) = \frac{K}{1 + be^{-rt}} \rightarrow (1) \]

เมื่อ 

t  = 0,1,2,3,...

P(t) คือจำนวนประชากร ณ t ใด ๆ 

r  คืออัตราการเพิ่มของประชากร มีค่าคงที่ ณ ช่วงเวลาที่สนใจ

K คือ จำนวนประชากรสูงสุด (carrying capacity)

b = \( \frac{K- P(0)}{P(0)}\)

e = Euler's number (~ 2.71828)

ตัดวันที่จำนวนคนติดเชื้อเป็น 0 ออกไป จะได้ว่าประชากร (ในที่นี้คือจำนวนผู้ติดเชื้อ) จำนวนเริ่มต้นคือ 6 ราย และจำนวนประชากรสูงสุดคือ 3062 ราย นำมากำหนดเป็นค่าคงที่สำหรับสมการได้ดังนี้

K = 3062

P(0)  = 6 

\( \therefore  b = \frac{3062 - 6}{6} = 509.33\)

สิ่งที่เหลือให้เราต้องการประมาณค่า  r หรืออัตราการเพิ่มของคนติดเชื้อในระหว่างเวลาที่เรามีข้อมูล 

เพิ่มเติม :

จาก  (1)  พิจารณาเฉพาะส่วน \( -rt \) เราอาจพิจารณาเขียนในรูปแบบใหม่คือ \( -rt = -xt + y \)

หรือเราสามารถเขียน (1) ในอีกรูปหนึ่งคือ \[ P(t) = \frac{K}{1 + be^{y - xt} } \rightarrow (2) \]

 จาก (2) มาดูว่า x และ y  จะมีผลอย่างไรต่อรูปแบบของกราฟ โดยใช้ข้อมูลสมมุติ

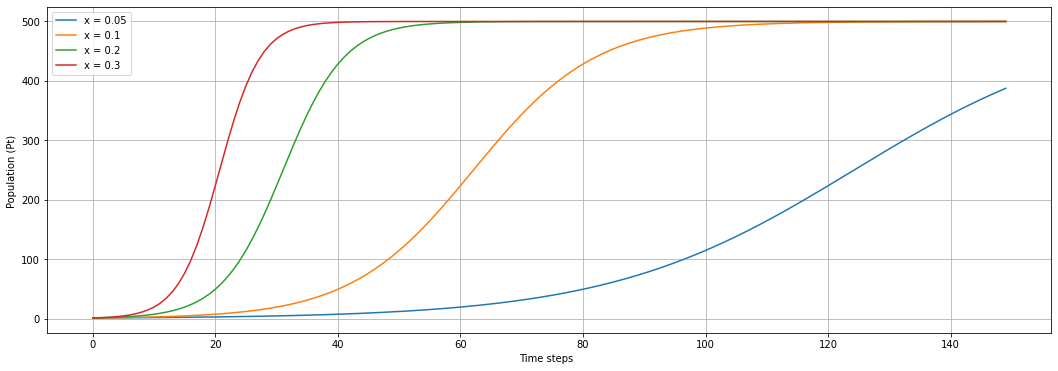รูปที่ 2 

รูปที่ 2 แสดงความสัมพันธ์ระหว่างค่า x กับความชัน ถ้ากำหนดให้ y คงที่ เมื่อ x มีค่าเปลี่ยนไป ความชันของกราฟก็จะเปลี่ยนตามไปด้วย

 รูปที่ 3  

รูปที่ 3 แสดงให้เห็นความสัมพันธ์ของ y เมื่อกำหนดค่า x คงที่ แต่เปลี่ยนค่า y สิ่งที่เปลี่ยนไปคือตำแหน่งของกราฟที่มีการเปลี่ยนความชันอย่างรวดเร็ว หรืออาจมองว่าค่าของ y ส่งผลต่อการขยับตำแหน่งของกราฟ แต่ไม่กระทบต่อความชัน

รูปที่ 4

รูปที่ 4 สรุปให้เห็นความสัมพันธ์ระหว่างค่า x,y กับรูปแบบของเส้นกราฟ เราอาจสรุปได้ว่าการประมาณค่า parameter สำหรับกราฟนั้นคือความพยายามในการปรับค่าของ x,y ไปเรื่อย ๆ จนรูปของเส้นกราฟมีความใกล้เคียงกับกราฟที่ได้จากข้อมูลสังเกตุก็ได้ 

กระบวนการทำงาน

1. สร้าง Lookup table

ตามที่ได้บอกไว้ก่อนหน้านี้ fitness function ถือเป็นหัวใจสำคัญของ GA เราต้องการบางอย่างเพื่อนำไปใช้ใน fitness function เพื่อใช้บอกว่า Individual นั้นเหมาะสมแค่ไหน 

Lookup table คือข้อมูลที่อยู่ในโครงสร้างแบบเดียวกับตาราง ซึ่งเราจะใช้ประโยชน์ในการเทียบค่าระหว่างค่าของสมการที่ได้จากการค้นหาด้วย GA กับค่าที่เกิดขึ้นจริงจากการสังเกตุ

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# parameters
K = 3062
P0 = 6
b = (K-P0)/P0
data = pd.read_csv('covid_thailand.csv')
lookup_table = {}
for i, row in data.iterrows():
    lookup_table[row['t']]=row['cases']
    
  

2. สร้างตัวแทนของ Individual

class Individual():
    def __init__(self):
        # chromosome contains 2 elements represent [x,y]
        self.chromosome = [np.random.rand() ,np.random.normal()]
        
        
    def fitness(self):
        se = 0.0 # sum of error
        for x in lookup_table.keys():
            generated = K / (1 + b * np.exp(-self.chromosome[0] * x + self.chromosome[1]))        
            observed = lookup_table[x]
            se += abs(observed - generated)
            
        # fitness is average of error    
        f = se/len(lookup_table) 
        return f

class Individual มีส่วนสำคัญสองส่วน คือ chromosome ใช้แทน parameter ในสมการคือ ตัวแปร   x,y ตามสมการที่ (2)

3.  GA 

class GA():
    def __init__(self,pop_size):
        self.population = []
        self.pop_size = pop_size
        self.k = 3
        self.elitism_rate = 0.05
        self.mutation_rate = 0.01
        
        # generate first generation
        g0 = []
        for i in range(self.pop_size):
            g0.append(Individual())
        self.population = self.sort(g0)
        
    def select(self):
        # do use tournament selection
        s1 = np.random.choice(self.population,size=self.k,replace=False)
        best = None
        for s in s1:
            if best is None or s.fitness() > best.fitness():
                best = s
        return best
    
    def crossover(self,ind1,ind2):
        new_chrom = []
       
        #play coin tossing 
        p = np.random.rand()
        if p < 0.5 :
            new_chrom.append(ind1.chromosome[0])
            new_chrom.append(ind2.chromosome[1])
        else:
            new_chrom.append(ind2.chromosome[0])
            new_chrom.append(ind1.chromosome[1])

            
        offspring = Individual()
        offspring.chromosome = new_chrom
        return offspring
    
    def mutate(self,ind):
        # do a little bit change in value of each gene
        new_chrom = []
        b = ind.chromosome[0]
        r = ind.chromosome[1]
        
        b_lowest = b - self.mutation_rate
        b_highest = b + self.mutation_rate
        
        # new b must be range between b_lowest and b_highest
        b = np.random.uniform(b_lowest,b_highest)
        
        r_lowest = r - self.mutation_rate
        r_highest = r + self.mutation_rate
        
        # new r must be range between r_lowest and r_highest
        r = np.random.uniform(r_lowest,r_highest)
                
        ind.chromosome[0] = b
        ind.chromosome[1] = r
        
        return ind
    
    def sort(self,population):
        return sorted(population,key=lambda x:x.fitness())
    
    def elitism(self):
        elite=[]
        elite_size = round(self.pop_size * self.elitism_rate)
        
        # pick up the best
        elite.extend(self.population[:elite_size])
        
        return elite
    
    
        
    def evolute(self):
        # get elite from ancester
        gt = self.elitism()        
        
        while len(gt) < self.pop_size :
            # get parent
            p1 = self.select()
            p2 = self.select()
            
            # crossover and mutation
            offspring = self.crossover(p1,p2)
            offspring = self.mutate(offspring)
            
            # put new one onto the population
            gt.append(offspring)
        
        #move to next generation
        self.population = self.sort(gt)
        
        
    def get_the_best(self):
        # the best is the one with lowest fitness
        return self.population[0]       

พิจารณา code ในส่วนของการทำ mutation ในตัวอย่างนี้อาจดูแล้วไม่เหมือนกับการ swap gene แบบที่เคยทำในตัวอย่าง เกมส์ทายคำ แต่ขอพิจารณาว่า ในกรณีนี้ gene set คือ real number ดังนั้นการเปลี่ยนแปลงของ gene ในแบบที่เขียนไว้ใน code นี้ก็เป็นการ swap gene แบบหนึ่งเช่นกัน เพียงแต่ว่าไม่ได้ระบุ gene set ให้เห็นชัดเจน แต่ใช้การตีความจากบริบทของปัญหา

4. ทดสอบ

  
ga = GA(100)
ga.elitism_rate = 0.2
ga.mutation_rate = 0.05
epochs = 1000
epoch = 0
log = []
best = ga.get_the_best()
while epoch < epochs and best.fitness() > 10:
    ga.evolute()
    best = ga.get_the_best()
    epoch += 1
    if epoch % 50 == 0 :
        fn = ga.get_the_best().fitness()
        log.append(fn)
        print("Epoch : {}, best fitness : {}".format(epoch,fn))
print("Epoch : {}, best fitness : {}".format(epoch,fn))   
  
  

สังเกตุว่าค่าของ fitness เหมือนจะไม่เปลี่ยนแปลงมาระยะหนึ่งแล้ว (แต่จริงๆ แล้วไม่ทราบได้ ถ้ามีเวลาก็สามารถทำต่อไปได้เรื่อย ๆ) ลองหยุดการทำงานแล้วมาดูผลกัน

รูปที่ 5 แสดงการเปลี่ยนแปลงค่าของ Fitness (Error)

import matplotlib.pyplot as plt

t =[]
pt =[]
best = ga.get_the_best()
print(best.chromosome)
for x in lookup_table.keys():
    t.append(x)
    pt.append(K/(1 + b * np.exp(-best.chromosome[0] * x + best.chromosome[1]) ))

t1=[]
pt1=[]
for k,v in lookup_table.items():
    t1.append(k)
    pt1.append(v)
    
plt.figure(figsize=(24,8))
plt.plot(t,pt,label="Estimated")
plt.plot(t1,gaussian_filter1d(pt1,sigma=1.5),label="Observed")
plt.grid(True)
plt.legend()
plt.show()

รูปที่ 6 กราฟที่ได้จากประมาณค่าพารามิเตอร์ (สีน้ำเงิน) กับค่าที่ได้จากรายงาน (สีส้ม) 

ได้ค่าประมาณของ x,y คือ [0.14495469994715768, 2.324099411100931] ตามลำดับ ดังนั้น curve estimation สมการเพื่อหาการเพิ่มขึ้นของจำนวนคนติดเชื้อ Covid-19 ของไทยช่วงระหว่ง  1 ก.พ. ถึง 31 พ.ค. คือ

\[ P(t) = \frac{3206}{1+509.33 e^{-0.145t + 2.324}}\]

แนวทางปรับแต่ง

GA กำหนดแนวทางไว้ให้ แต่ไม่ได้บังคับว่าต้องทำตามทุกอย่าง เราสามารถปรับเปลี่ยนได้ 

ปรับแต่งขั้นตอน selection 

  def tricky_select(self):        
        good_idx = round(self.pop_size*0.5)
        s1 = np.random.choice(self.population[:good_idx],size=self.k,replace=False)
        best = None
        for s in s1:
            if best is None or s.fitness() > best.fitness():
                best = s
        return best

code ส่วนนี้มีการเปลี่ยนแปลงขั้นตอนการทำ selection นิดหน่อย เราทราบว่ามี Individual บางส่วนที่มี Fitness ที่ดีอยู่ เราก็เลือกมาเฉพาะส่วนที่ดีมาแทนที่การเลือกจาก population ทั้งหมด เพื่อตีกรอบการคัดเลือกลง ในตัวอย่างใช้การลดจำนวน population ลงครึ่งหนึ่งภายใต้สมมุติฐานว่าครึ่งที่เอามาใช้จะให้ผลที่ดีกว่ากลุ่มในครึ่งหลัง ท่านสามารถปรับเปลี่ยนตัวเลขได้ตามใจเพื่อศึกษาผลกระทบที่ได้

ปรับแต่ง mutation 

เป้าหมายหลักหนึ่งของ GA  คือการปรับตัวให้ดีขึ้น การ mutation เป็นกระบวนหนึ่งที่ออกแบบมาเพื่อสนับสนุนแนวคิดนี้  การปล่อยให้เกิด mutation ให้เป็นไปตามความน่าจะเป็นอาจไม่ดีขึ้นเสมอไป บางครั้งก็ต้องลงมือช่วย

import copy

def mutate(self,ind):
        c1 = copy.deepcopy(ind)
        c2 = copy.deepcopy(ind)
        
        c1.chromosome[0] = np.random.uniform(c1.chromosome[0]-self.mutation_rate ,c1.chromosome[0])
        c2.chromosome[0] = np.random.uniform(c2.chromosome[0] ,c2.chromosome[0] + self.mutation_rate)
        
        if c1.fitness() < ind.fitness():
            ind = c1
        elif c2.fitness() < ind.fitness():
            ind = c2        
        
        return ind

ยืมมือการทำ deepcopy มาใช้ (การทำ deepcopy อยู่นอกเหนือขอบเขตของเนื้อเรื่องจะขอข้ามไปก่อน) แนวคิดของ code ชุดนี้คือ ทำสำเนาหรือ clone Individual แล้วนำไปปรับแต่ง chromosome แล้วเลือกเอา clone ที่ให้ fitness ที่ดีกว่าส่งต่อไป

ปรุ่งแต่งใหม่

เพื่อให้เห็นภาพชัดขึ้นขอกลับไปที่สมการที่ (1) และ (2)  ใน (1) เป็นแบบมาตรฐาน แต่ (2) เป็นแบบที่ปรับแต่งเพื่อให้เหมาะกับการใช้ GA  แม้จะได้สมการ หรือสูตร ที่สามารถสร้างกราฟที่ใกล้เคียงกับค่าสังเกตุแต่ก็ตีความอยาก เพราะค่า rt ใน (1)  นั้นมีความหมายในทางระบาดวิทยามากกว่าการตีความจาก y - xt 

แต่ถ้าเราใช้การประมาณค่า r ตัวเดียวในกรณีนี้ ก็เหมือนกับว่า chromosome จะมีเพียง gene เดียว ซึ่งไม่จำเป็นต้องใช้ขั้นตอน crossover ก็ได้ ข้ามไปสู่การ mutation เลย มองมุมนี้รูปแบบการทำงานจะคล้ายกับการทำงานของ Neural Network 

import copy

class NO_crossover_Individual():
    def __init__(self):
        # chromosome contains 1 elements representing [r]
        self.chromosome = [np.random.rand()]
        
        
    def fitness(self):
        se = 0.0 # sum of error
        for x in lookup_table.keys():
            generated = K / (1 + b * np.exp(-self.chromosome[0] * x ))        
            observed = lookup_table[x]
            se += abs(observed - generated)
            
        # fitness is average of error    
        f = se/len(lookup_table) 
        return f
        

class NO_crossover_GA():
    def __init__(self,pop_size):
        self.population = []
        self.pop_size = pop_size
        self.k = 3
        self.elitism_rate = 0.05
        self.mutation_rate = 0.01
        
        # generate first generation
        g0 = []
        for i in range(self.pop_size):
            g0.append(NO_crossover_Individual())
        self.population = self.sort(g0)    
    
    def select(self):
        # do use tournament selection
        good_idx = round(self.pop_size*0.5)
        s1 = np.random.choice(self.population[:good_idx],size=self.k,replace=False)
        best = None
        for s in s1:
            if best is None or s.fitness() > best.fitness():
                best = s
        return best    
    
    def mutate(self,ind):
        # do a little bit change in value of each gene
        c1 = copy.deepcopy(ind)
        c2 = copy.deepcopy(ind)
        
        c1.chromosome[0] = np.random.uniform(c1.chromosome[0]-self.mutation_rate ,c1.chromosome[0])
        c2.chromosome[0] = np.random.uniform(c2.chromosome[0] ,c2.chromosome[0] + self.mutation_rate)
        
        if c1.fitness() < ind.fitness():
            ind = c1
        elif c2.fitness() < ind.fitness():
            ind = c2        
        
        return ind
    
    def sort(self,population):
        return sorted(population,key=lambda x:x.fitness())
    
    def elitism(self):
        elite=[]
        elite_size = round(self.pop_size * self.elitism_rate)
        
        # pick up the best
        elite.extend(self.population[:elite_size])
        
        return elite
    
    
        
    def evolute(self):
        # get elite from ancester
        gt = self.elitism()        
        while len(gt) < self.pop_size :
            offspring = self.select()
            offspring = self.mutate(offspring)
            
            # put new one onto the population
            gt.append(offspring)
        
        #move to next generation
        self.population = self.sort(gt)
        
        
    def get_the_best(self):
        # the best is the one with lowest fitness
        return self.population[0]       
  
  
ns_ga = NO_crossover_GA(10)
ns_ga.elitism_rate = 0.1
ns_ga.mutation_rate = 0.05
epochs = 100
epoch = 0
ns_log = []
ns_best = ns_ga.get_the_best()
print("Epoch : {}, best fitness : {}".format(epoch,ns_best.fitness()))     
while epoch < epochs and round(ns_best.fitness()) > 50 :
    ns_ga.evolute()
    ns_best = ns_ga.get_the_best()
    epoch += 1
    if epoch % 10 == 0 :
        fn = ns_best.fitness()
        ns_log.append(fn)
        print("Epoch : {}, best fitness : {}".format(epoch,fn))
print("Epoch : {}, best fitness : {}".format(epoch,ns_best.fitness()))     
  

ดูเหมือนจะดีขึ้น เพราะเราใช้จำนวนประชากรลดลงได้ และได้จำนวน iteration ในการ evolution ลดลงด้วย สังเกตุคอลัมน์สุดท้าย epoch ที่ 20 ได้ค่า fitness ที่ลดลงวูบวาบ ทดลองหลายครั้งก็ได้ผลทำนองเดียวกัน แม้ตัวเลขจะต่างกันไป เพราะครั้งแรกของการสร้างประชากรจะสร้างแบบสุ่ม มองโดยรวมแล้วการปรับแต่งคงจะให้ผลที่ดีขึ้นในแง่เวลาและทรัพยากร มาดูผลการสร้างกราฟกันบ้าง ก็ได้ผลไม่แตกต่างจากการทำงานในครั้งแรกๆ มากนัก และเราก็ได้สมการใหม่สำหรับการทำนายลักษณะการแพร่ระบาดเป็น

\[ P(t) = \frac{3062}{1+ 509.33 e^{-0.105t}}\]

สรุป

1. ข้อเขียนนี้เพียงต้องการยกตัวอย่างให้เห็นว่าหลักการของ Genetic algorithm สามารถนำไปประยุกต์กับสถานการณ์จริงได้อย่างไร ไม่ใช่แต่เฉพาะกับ toy data

 

2. ข้อเขียนนี้ไม่ได้เสนอว่านี่คือขั้นตอนที่เป็นมาตรฐานต้องทำแบบนี้ การแก้ปัญหาขึ้นกับผู้ตีความปัญหา การประยุกต์สิ่งที่มีอยู่ให้นำไปสู่การแก้ปัญหาเท่านั้น

3. กรุณาอย่านำค่าที่ได้จากการประมาณการในข้อเขียนนี้ไปอ้างอิงที่อื่น เพราะไม่มีการรับรองใดๆทั้งสิ้น 

4. download source code

เอกสารอ้างอิง

[1] https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_daily_reports

[2] https://en.wikipedia.org/wiki/Sigmoid_function

[3] https://en.wikipedia.org/wiki/COVID-19_pandemic

[4] https://smarter-machine.blogspot.com/2020/04/logistic-growth.html