 |
โยน 1 ลูก เซตของหน้าลูกเต๋าที่หงายขึ้น Sample space คือ
\[ S = \{1,2,3,4,5,6 \}\]
ถ้ากำหนดให้ A แทนเหตุการณ์ของหน้าลูกเต๋าที่หงายขึ้นเป็นเลขคี่ จะได้
\[ \begin{align*} A &= \{ 1,3,5\} \\ P(A) &= \frac{\mid A \mid}{\mid S \mid} \\ \therefore P(A) &= \frac{3}{6} = \frac{1}{2} \end{align*} \]
และกำหนด B แทนเหตุการณ์ที่หน้าลูกเต๋าที่หงายมีค่าน้อยกว่า 4 จะได้
\[ \begin{align*} B &= \{ 1,2,3 \} \\ P(B) &= \frac{\mid B \mid}{\mid S \mid} \\ \therefore P(B) &= \frac{3}{6} = \frac{1}{2} \end{align*} \]
ถ้าเราสนใจหาความน่าจะเป็นของเหตุการณ์ที่เป็นเงื่อนไขต่อกัน เช่น สนใจเหตุการณ์ที่หน้าลูกเต๋าหงายเป็นเลขคี่และเหตุการณ์ที่หน้าลูกเต๋ามีค่าน้อยกว่า 4 ในการคำนวณ เราต้องการตีกรอบเหตุการณ์ให้แคบลงมาเหลือเฉพาะที่เป็นเลขคี่ก่อน คือ \( {1,3,5 }\) แล้วมองหาจำนวนเหตุการณ์ที่สองคือเลขคี่ที่น้อยกว่า 4 ถ้าให้ C แทนเหตุการณ์ที่ระบุด้วยเงื่อนไขนี้
\[ C = A \cap B = \{ 1,3 \}\]
และเนื่องจากเราจำกัดวงของเหตุการณ์ให้แคบลงเหลือแค่ในขอบเขตของเหตุการณ์ B ดังนั้นในการหาค่าความน่าจะเป็นของ C จึงต้องใช้ sample space ที่เป็น B แทนที่ S
 |
| รูปที่ 1 |
\[ \begin{align*} P(C) &= \frac{\mid C \mid}{\mid B \mid} \\ P(C) &= \frac{\mid A \cap B \mid}{\mid B \mid} \\ P(C) &= \frac{2}{3} \\ \end{align*} \]
เราเรียกเหตุการณ์ \(P(C) \) นี้ว่าเป็นค่าความน่าจะเป็นแบบมีเงื่อนไข (conditional probability of A given B) เขียนแทนด้วย \( P(A \mid B) \)
\[ \begin{align*} P(A \mid B) &= \frac{\mid A \cap B \mid}{\mid B \mid} \\ P(A \mid B) &= \frac{\frac{\mid A \cap B \mid}{\mid S \mid}}{\frac{\mid B \mid}{\mid S \mid}} \\ P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\ \end{align*} \]
นำไปสู่ข้อสรุปที่ว่า
"If A and B are events in same sample space, then conditional probability of A given B is defined as"
\[ \begin{equation} \boxed{ P(A \mid B) = \frac{P(A \cap B)}{P(B)} }\tag{1.0} \end{equation} \]
กรณีพิเศษ
1. ถ้า A และ B เป็นเหตุการณ์ที่เป็นอิสระต่อกัน (disjoint) \(A \cap B = \emptyset \) จะได้
\[ \begin{align*} P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\ P(A \mid B) &= \frac{P(\emptyset)}{P(B)} \\ P(A \mid B) &= \frac{0}{P(B)} \\ \therefore P(A \mid B) &= 0 \end{align*} \]
2. ถ้า A อยู่ใน B ( \(A \subset B \) )
\[ \begin{align*} P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\ \therefore P(A \mid B) &= \frac{P(A)}{P(B)} \\ \end{align*} \]
3. ถ้า B อยู่ใน A ( \(B \subset A \) )
\[ \begin{align*} P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\ P(A \mid B) &= \frac{P(B)}{P(B)} \\ \therefore P(A \mid B) &= 1.0 \\ \end{align*} \]
ตัวอย่าง ในการสำรวจลูกค้าที่ซื้อรถยนต์ของบริษัท A ไปจำนวน 100 ราย พบว่า มี 40 รายที่ซื้ออุปกรณ์เสริมเป็นระบบสัญญาณกันขโมยอย่างเดียว มี 30 รายที่ซื้อ car seat สำหรับเด็กอย่างเดียว และมี 20 รายที่ซื้อทั้งสองรายการ ที่เหลือไม่ได้ซื้ออุปกรณ์ใด ถ้าสุ่มเลือกลูกค้ากลุ่มนี้มา 1 รายจากกลุ่มที่ได้ซื้อระบบสัญญาณกันขโมยไป probability ที่ลูกค้ารายนี้จะเป็นลูกค้าที่ซื้อ car seat ไปด้วยมีค่าเท่าใด
 |
ให้ X แทนเหตุการณ์ที่ลูกค้าซื้ออุปกรณ์เสริมเป็นระบบสัญญาณกันขโมยอย่างเดียว
ให้ Y แทนเหตุการณ์ที่ลูกค้าซื้ออุปกรณ์เสริมเป็น car seat อย่างเดียว
การเลือกลูกค้า 1 แบบสุ่มจากกลุ่มลูกค้าที่ได้ซื้อระบบสัญญาณกันขโมยไป เงื่อนไขนี้ทำให้เราตีกรอบให้มองไปในพื้นที่ลูกค้าที่อยู่ในกลุ่ม X เท่าน้น แล้วมองดูว่าลูกค้ากลุ่มนี้มีจำนวนเท่าใดที่ได้ซื้อ car seat ไปด้วย หรือ โจทย์ได้ถามหา \( P(Y \mid X) \)
จากกำหนดมา
\[ \begin{align*} P(X) &= \frac{40}{100} = 0.4 \\\\ P(X \cap Y) &= 0.2\\\\ \end{align*} \]จาก (1.0)
\[ \begin{align*} P(Y \mid X) &= \frac{P(X \cap Y)}{P(X)} \\\\ P(Y \mid X) &= \frac{0.2}{0.4} \\\\ P(Y \mid X) &= 0.5 \\\\ \end{align*} \]ขอให้สังเกตุว่ามีความต่างกันหากโจทย์ถามว่า "เลือกลูกค้าแบบสุ่มมา 1 คน โอกาสที่ที่ลูกค้ารายนี้จะเป็นลูกค้าที่ซื้อทั้งสองรายการเป็นเท่าใด" คำตอบควรเป็น 0.2 ที่ต่างคือโจทย์ได้กำหนดเหตุการณ์ที่เป็นเงื่อนไขขึ้นมาก่อนแล้วจึงถามหาความน่าจะเป็นของเหตุการณ์ที่ซ้อนเข้าไป
ตัวอย่าง ครอบครัวที่มีบุตร 2 คน Sample space ของเพศของบุตรทั้งสองคือ \[ \S = \{(ชาย,ชาย),(ชาย,หญิง),(หญิง,หญิง),(หญิง,ชาย) \}\] คำนวณหาความน่าจะเป็นของเหตุการณ์
1. เลือกครอบครัวจากกลุ่มที่มีบุตรคนแรกเป็นหญิง ความน่าจะเป็นที่ครอบครัวนั้นจะมีบุตรคนที่สองเป็นหญิง
2. เลือกครอบครัวจากกลุ่มที่มีบุตรเป็นหญิงอย่างน้อย 1 คน ความน่าจะเป็นที่ครอบครัวนั้นจะมีบุตรคนที่สองเป็นหญิง
ให้ A แทน เหตุการณ์ลูกคนแรกเป็นหญิง \( P(A) = \frac{1}{2} \)
ให้ B แทน เหตุการณ์ลูกคนที่สองเป็นหญิง \(P(B) = \frac{1}{2} \)
ได้ \( B \cup A \) คือเหตุการณ์ที่ลูกทั้งสองคนเป็นหญิง \( P(A \cup B) = \frac{1}{4}\)
จะได้ \(B \mid A \) คือเหตุการณ์ที่ลูกคนที่สองเป็นหญิง เมื่อทราบแล้วว่าลูกคนแรกเป็นหญิง
ข้อ 1. \[ \begin{align*} P(B \mid A) &= \frac{P(B \cap A)}{P(A)} \\ P(B \mid A) &= \frac{\frac{1}{4}}{\frac{1}{2}} \\ \therefore P(B \mid A) &= \frac{1}{2} \\ \end{align*} \]
ข้อ 2 .
ให้ A แทนเหตุการณ์ลูกอย่างน้อยหนึ่งคนเป็นหญิง, \( P(A) = \frac{3}{4} \)
ให้ B แทนเหตุการณ์ลูกคนที่สองเป็นหญิง \(P(B) = \frac{1}{2} \)
ได้ \( B \cup A \) คือเหตุการณ์ที่ลูกทั้งสองคนเป็นหญิง \( P(A \cup B) = \frac{1}{4}\)
จะได้ \(B \mid A \) ลูกคนที่สองเป็นหญิง เมื่อทราบแล้วว่ามีลูกหญิงแล้วอย่างน้อย 1 คน
\[ \begin{align*} P(B \mid A) &= \frac{P(B \cap A)}{P(A)} \\ P(B \mid A) &= \frac{\frac{1}{4}}{\frac{3}{4}} \\ \therefore P(B \mid A) &= \frac{1}{3} \\ \end{align*} \]
Chain rule for conditional probability
\[ \begin{align*} P(A \mid B) &= \frac{P(A \cap B)}{P(B)} \\\\ P(A \cap B) &= P(A \mid B)P(B) \tag{2.1}\\ \end{align*} \]
และ
\[ \begin{align*} P(B \mid A) &= \frac{P(B \cap A)}{P(A)} \\\\ P(B \cap A) &= P(B \mid A)P(A) \tag{2.2}\\ \end{align*} \]
เนื่องจาก \( P(A \cap B) = P(B \cap A) \) ดังนั้น
\[ \boxed{ P(A \cap B) = P(B \mid A)P(A) = P(A \mid B)P(B) }\tag{2.3} \]
 |
| รูปที่ 1 พื้นที่ที่ใช้แทนความน่าจะเป็นของเหตุการณ์ \( A \cap B \) |
ลองเพิ่มจำนวนเหตุการณ์เข้าเป็นสามเหตุการณ์ที่เกิดขึ้นร่วมกันแบบมีเงื่อนไข \( P( A \cap B \cap C) = ?\)
 |
| รูปที่ 2 |
พิจารณารวมเหตุการณ์จาก 3 เหลือ 2 เหตุการณ์โดยการรวมกลุ่ม
\[ \begin{align*} P(A \cap B \cap C) &= P(A \cap (B \cap C)) \\ P(A \cap B \cap C) &= P(A) \cdot P( B \cap C \mid A) \tag{2.4}\\ \end{align*} \]
พิจารณาดูว่า \(P(B \cap C) \mid A ) \) หาได้อย่างไร ?
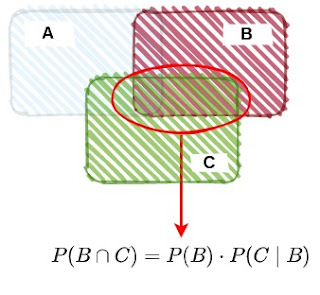 |
| รูปที่ 3 |
ดูรูปที่ 3 \(P(B \cap C) \) คือพื้นที่ในวงสีแดง ดังนั้น \(P(B \cap C) \mid A )\) จึงตีความได้ว่า คือพื้นที่ของเหตุการณ์ \( B \cap C \) ภายใต้เงื่อนไขที่ต้องมีเหตุการณ์ A เกิดขึ้นมาก่อน เขียนแทนด้วย \( P(B \cap C \mid A) \)
และเราทราบว่า
\[ \begin{align*} P(B \cap C) &= P(B) \cdot P(C \mid B ) \\ P(B \cap C \mid A) &= P(B \mid A) \cdot P(C \mid A,B ) \tag{2.5}\\ \end{align*} \]
นำค่าจาก \(( 2.5) \) ไปแทนใน \( (2.4) \)จะได้
\[ \begin{align*} P(A \cap B \cap C) &= P(A) \cdot P( B \cap C \mid A) \\ P(A \cap B \cap C) &= P(A) \cdot P(B \mid A) \cdot P(C \mid A,B ) \tag{2.6}\\ \end{align*} \]
พิจารณา \((2.6) \) (อาจดูยากสักหน่อย แต่ลองพยายามดู) ถ้าหากเพิ่มจำนวนเหตุการณ์ D เป็นเหตุการณ์ที่ 4 เข้าไป สมการที่ได้ก็ควรจะเป็น
\[ \begin{align*} P(A \cap B \cap C \cap D) &= P(A) \cdot P(B \mid A) \cdot P(C \mid A,B ) \cdot P(D \mid A,B,C) \\ \end{align*} \]
ถ้าหากเพิ่มจำนวนเหตุการณ์ E เป็นเหตุการณ์ที่ 5 เข้าไป สมการที่ได้ก็ควรจะเป็น
\[ \begin{align*} P(A \cap B \cap C \cap D \cap E) &= P(A) \cdot P(B \mid A) \cdot P(C \mid A,B ) \cdot P(D \mid A,B,C) \cdot P(E \mid A,B,C,D)\\ \end{align*} \]
นำไปสู่ข้อสรุปรูปแบบสมการทั่วไปดังนี้
\[ \small{ P(A_1 \cap A_2 \cap A_3 \cap \cdots \cap A_n) = P(A_1) \cdot P(A_2 \mid A_1) \cdot P(A_3 \mid A_1,A_2 ) \cdots P(A_n \mid A_1,A_2,A_3,...,A_{n-1}) } \tag{2.7} \]
เรียกสมการ \((2.7) \) ว่าเป็น Chain rule for conditional probability
ตัวอย่าง สมมุติว่ามีการระบาดของโรคร้ายชนิดหนึ่ง จากการสำรวจทำให้ทราบว่า ผู้ติดเชื้อโรคนี้จะมีอาการรุนแรง 5 % ถ้าทำการเลือกผู้ติดเชื้อแบบสุ่มทีละคนจำนวน 3 คนจากผู้ติดเชื้อ 100 คน หนึ่งเพื่อตรวจสอบ ความน่าจะเป็นในการที่จะเลือกได้ผู้ติดเชื้อมีอาการทั้งสามคนคือเท่าใด
กำหนดให้ \(A_1 \) แทนเหตุการณ์ผู้ติดเชื้อรายแรกเป็นผู้ป่วยมีอาการรุนแรง
กำหนดให้ \(A_2 \) แทนเหตุการณ์ผู้ติดเชื้อรายที่สองเป็นผู้ป่วยมีอาการรุนแรง
กำหนดให้ \(A_3 \) แทนเหตุการณ์ผู้ติดเชื้อรายที่สามเป็นผู้ป่วยมีอาการรุนแรง
จะได้ว่า \( P(A_1) \) คือความน่าจะเป็นที่ผู้ติดเชื้อรายแรกเป็นผู้ป่วยมีอาการรุนแรง
\( P(A_2 \mid A_1) \) คือความน่าจะเป็นที่ผู้ติดเชื้อรายที่สองเป็นผู้ป่วยมีอาการรุนแรงเมื่อที่ผู้ติดเชื้อรายแรกเป็นผู้ป่วยมีอาการรุนแรง
และ \( P(A_3 \mid A_1,A_2) \) คือความน่าจะเป็นที่ผู้ติดเชื้อรายที่สามเป็นผู้ป่วยมีอาการรุนแรงเมื่อที่ผู้ติดเชื้อรายแรกและรายที่สองเป็นผู้ป่วยมีอาการรุนแรง
สิ่งที่ต้องการหาคือ \( P(A_1 \cap A_2 \cap A_3 \) = ?
จากกำหนดให้ผู้ติดเชื้อ 100 คนประกอบด้วยสองส่วนคือ 5 คนมีอาการรุนแรงและ 95 คนมีอาการไม่รุนแรง
 |
การที่จะเลือกผู้ติดเชื้อรายแรกแล้วจะได้เป็นผู้ติดเชื้อที่มีอาการรุนแรง จะต้องได้มาจากส่วนที่เป็น 5 คน จากผู้ติดเชื้อทั้งหมด 100 คน เท่านั้น นั่นคือ
\[ \therefore P(A_1) = \frac{5}{100} \tag{3.1} \]
หลังจากเลือกผู้ติดเชื้อรายแรกไปแล้ว จะเหลือผู้ติดเชื้อทั้งหมด 99 คน และการที่จะเลือกคนที่สองแล้วได้ผู้ติดเชื้อที่มีอาการรุนแรง จะต้องเลือกมาจากส่วนที่ผู้ติดเชื้อมีอาการรุนแรง ซึ่งตอนนี้จะเหลือให้ 4 ราย นั่นคือ
\[ \therefore P(A_2 \mid A_1) = \frac{4}{99} \tag{3.2} \]
ทำนองเดียวกัน หลังจากเลือกผู้ติดเชื้อสองไปแล้วจะเหลือผู้ติดเชื้อทั้งหมด 98 คน และการที่จะได้ผู้ติดเชื้อรายที่สามเป็นผู้ติดเชื้อที่มีอาการรุนแรงอีกก็ต้องมาจากส่วนที่เป็นผู้ติดเชื้ออาการรุนแรงอีก ซึ่งตอนนี้จะเหลือ 3 คน นั่นคือ
\[ \therefore P(A_2 \mid A_1,A_2) = \frac{3}{98} \tag{3.3} \]
จาก \((2.7) \),
\[ \begin{align*} P(A_1 \cap A_2 \cap A_3 ) &= P(A_1) \cdot P(A_2 \mid A_1) \cdot P(A_3 \mid A_1,A_2) \\ \end{align*} \]
แทนค่าที่ได้จาก (3.1),(3.2),(3.3)
\[ \begin{align*} P(A_1 \cap A_2 \cap A_3 ) &= \frac{5}{100} \times \frac{4}{99} \times \frac{3}{98} \\ \therefore P(A_1 \cap A_2 \cap A_3 ) &= \frac{1}{16170} \\ \end{align*} \]

ความคิดเห็น
แสดงความคิดเห็น