การไหลในเครือข่าย (network flow) ถูกใช้ในศึกษาในหลายระบบ ตัวอย่างหนึ่งคือระบบระบายน้ำในเมือง ดังแสดงในรูปที่ 1 เส้นทางน้ำไหล (เส้นสีนำ้เงินเข้ม) มีการเชื่อมต่อกันเป็นข่ายงาน (network) สิ่งที่ไหล (flow) ภายในคือน้ำ คลองแต่ละเส้นจะมีความจุหรือความสามารถในการระบายน้ำ(capacity) ที่แน่นอน น้ำที่ไหลอยู่ในระบบจะมีทิศทางการไหลจากแหล่งกำเนิด (source) ผ่านไปยังส่วนต่างๆ แล้วไหลไปรวมกันยังปลายทาง (sink) เสมอ
 |
| รูปที่ 1 ส่วนหนึ่งของเส้นทางคลองระบายน้ำในกรุงเทพ ฯ แทนที่ด้วยเส้นสีน้ำเงินเข้ม |
เพื่อจะศึกษาเรื่องนี้ เราสร้างแบบจำลองที่เป็น directed graph ขึ้นมาเพื่อแทนตัวของ network (รูปที่ 2 ) ให้ weight edges แทนขนาดของ capacity และทิศทางการไหลของน้ำ ให้ vertices แทนจุดเชื่อมหรือจุดพักน้ำ จะเห็นว่ามี vertex ลักษณะพิเศษ 2 vertices คือ source (S) และ sink (T) โดยที่
‣ Source vertex มีแต่ edge ขาออก
‣ Sink vertex มีแต่ edge ขาเข้า
‣ Vertices ที่อยู่ระหว่าง มีได้ทั้ง edge ขาเข้าและขาออก
 |
| รูปที่ 2 |
นอกจากระบบระบบน้ำแล้วตัวแบบนี้อาจใช้กับระบบอะไรก็ได้ที่มีไหล (flow) ของวัตถุ เช่น ระบบจราจร ขนส่ง วงจรอิเล็กทรอนิกส์ เส้นทางการผลิตสินค้า ฯลฯ
Minimum cut problem
การ "cut" ในที่นี้หมายถึงการแบ่ง vertex ใน network ออกเป็น 2 กลุ่ม (สมมุติเป็น A,B) โดยที่ source vertex และ sink vertext จะอยู่คนละกลุ่ม ความจุของ cut คือ ผลรวมของ capacity ของ edges ที่ข้ามจากกลุ่ม A ไปยัง B
เมื่อ
\( cap(A,B) \) คือ capacity ทั้งหมดที่ไหลจากกลุ่ม A ไปยัง B
\( c(e) \) คือ capacity ของ edge แต่ละเส้นที่ไหลจาก A ไปยัง B ไม่นับที่ไหลจาก B ไปยัง A
ยกตัวอย่างเช่น
Cut 1 :
 |
| รูปที่ 3 |
Cut 2 :
 |
| รูปที่ 4 |
Cut 3 :
 |
| รูปที่ 5 |
Cut 4 :
 |
| รูปที่ 6 |
จากตัวอย่าง cut แบบที่ 4 ให้ค่า capacity ต่ำที่สุด (อาจมี cut แบบอื่นได้อีก ลองทำดู)
Maximum flow problem
ตัวแบบปัญหานี้คือการพยายามหาค่า flow ที่มากที่สุดที่จะผ่าน network หรือ flow มากที่สุดที่ไหลจาก source ไปยัง sink ในหนึ่งหน่วยเวลา

Terminology
• \( f(e) \) คือ flow ที่ไหลผ่าน e (edge)
• \( c(e) \) คือ capacity ของ e (edge)
• \( f(U,V) \) คือ flow จาก vertex U ไปยัง vertex V
• คุณสมบัติของ Flow
‣ \( f(e) \leq c(e) \) ,flow ไม่จำเป็นต้องมีค่าเท่ากับ capacity แต่มีค่าเกินไม่ได้
‣ \( f(U,V) = - f(V,U) \) (จะมี flow ที่ขนาดเท่ากันแต่มีทิศทางตรงข้าม)
‣ \( \sum_{\text{flow into V }}^{}f(e) = \sum_\text{flow outof V }f(e) \) (ค่าของ flow ขาออกจาก V รวมทั้งหมด จะต้องเท่ากับ flow ขาออกจาก V รวมทั้งหมด)
Ford-Fulkerson algorithm
เป็น greedy algorithm แบบหนึ่ง มีขั้นตอนโดยรวมดังนี้
1. เริ่มต้นโดยการกำหนดค่า flow ที่จะผ่านทุก edges ให้เป็น 0
.jpg) |
| รูปที่ 7 |
2. เลือกเส้นทางจาก source ไป sink สมมุติว่าเป็น \(S \rightarrow A \rightarrow B \rightarrow T \) เส้นทางที่เลือกไว้นี้เรียกว่า augmenting path
 |
| รูปที่ 7 |
นำค่า capacity ที่น้อยที่สุดในเส้นทางที่เลือก (ในกรณีนี้คือ 2) มาใช้เป็นค่าของ flow ของเส้นทางนี้ ในขั้นตอนนี้ได้ flow = 2
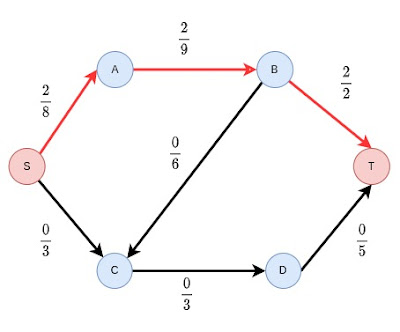 |
| รูปที่ 8 |
3. ทำซ้ำเหมือนในขั้นตอนที่ 2 คราวนี้ได้เส้นทาง \(S \rightarrow C \rightarrow D \rightarrow T \)
 |
| รูปที่ 9 |
ในขั้นตอนนี้หลังจากปรับค่าแล้ว ได้ flow = 3
จากรูปที่ 9 พิจารณาค่าของ \(\frac{\text{flow}}{\text{capacity}} \) พบว่ามี augmenting path ที่ \(\text{flow} = \text{capacity} \) แล้ว ได้แก่ \( B \rightarrow T, C \rightarrow D ,S \rightarrow C \) ความหมายคือ เส้นทางเหล่านี้ไม่สามารถนำมาช่วยเพิ่ม flow ให้กับ network ได้อีกแล้ว ถ้าลองตัดเส้นทางเหล่านี้ออกไปจาก network เพื่อจะหา path ที่เหลือว่ามีความเป็นไปได้ที่จะช่วยเพิ่ม flow หรือไม่ network ที่ได้จะเป็นดังรูปที่ 10
 |
| รูปที่ 10 |
จากรูปที่ 10 ทำให้ทราบว่าเป็นไม่ได้ที่จะเพิ่ม flow ให้กับ network อีกแล้ว ดังนั้น ผลลัพธ์สุดท้ายจะได้ค่า max flow เป็นผลรวมของ flow ที่ได้จากขั้นตอนที่ 2 และ 3 คือ 5
Max flow Min cut theorem
ถ้ากลับไปดูตัวเลขที่หาไว้ในตอนที่กล่าวเรื่อง minimum cut problem จะเห็นค่า min cut ของ network ตัวอย่างคือ 5 และเมื่อนำ graph เดียวกันมาหา max flow ก็ได้ 5 เช่นเดียวกัน ดังนั้นการทำ min cut มีประโยชน์ที่สามารถนำมาตรวจสอบว่าค่า max flow ที่ได้เป็นค่า max flow จริง

ความคิดเห็น
แสดงความคิดเห็น