Graph เป็นโครงสร้างทางคณิตศาสตร์แบบหนึ่งที่แสดงให้เห็นถึงความสัมพันธ์ระหว่าง object ประกอบขึ้นจากจุด (vertices หรือ nodes) ที่เชื่อมต่อกันผ่านเส้น (edges)
 |
| รูปที่ 1 |
Graph ไม่ได้สะท้อนภาพจริงแต่สะท้อนความสัมพันธ์ สามารถนำไปใช้ในสถานการณ์อื่นได้ เช่น web pages, social networking, map, database, chemistry, biology ฯลฯ ตัวอย่างในรูปที่ 1 ซ้ายมือคือแผนที่แสดงเส้นทางเดินของแม่น้ำสายหลักของไทยคือ ปิง วัง ยม น่าน ส่วนภาพด้านขวามือเป็น graph ที่ได้ข้อมูลจากแผนที่สะท้อนภาพของทิศทางการไหลของแม่น้ำ ต้นกำเนิด ตำแหน่งของการรวมตัว ฯล

Graph ใช้ศึกษาความสัมพันธ์ระหว่าง objects
Graph ประกอบด้วยองค์ประกอบที่เรียกว่า vertices หรือ node ที่เชื่อมต่อกันด้วย edge (รูปที่ 2) ถูกเขียนแทนด้วยคู่อันดับ (order pair)
เมื่อ
V คือ finite set ของ vertices
E คือ finite set ของ edges ซึ่งมักจะถูกเขียนในรูปแบบของ set ของคู่อันดับ
 |
| รูปที่ 2 |
รูปที่ 2 นำมาเขียนในรูปของเซตจะได้
\[ \begin{align*} V &= \{\text{เชียงใหม่},\text{ลำพูน},\text{ตาก}\} \\ E &= \{(\text{เชียงใหม่},\text{ลำพูน}),(\text{ลำพูน},\text{ตาก})\} \\ G &= (V,E) \end{align*} \]ชนิดของ Graph
Graph มีด้วยกันหลายชนิด ได้แก่
♦ Simple graph หรือ strict graph คือ graph ที่การเชื่อมกันของ 2 vertices ใดๆ ใช้เพียง edge เดียว เป็น graph ที่ไม่มี graph loops
♦ Directed graph คือ graph ที่ edges จะบอกถึงทิศทางทำให้ทราบจุดเริ่มต้นและจุดสิ้นสุด
♦ Undirected graph คือ graph ที่ edges ที่ไม่ได้บอกถึงทิศทาง
 |
| รูปที่ 3 |
♦ Weighted graph คือ graph ที่มีการระบุค่าให้กํบ edges เพื่อใช้บอกบางอย่าง เช่น ระยะทาง
 |
| รูปที่ 4 ตัวอย่าง Weighted graph ตัวเลขบน edge แทนระยะทางหน่วยเป็น กิโลเมตร |
♦ Complete graph เมื่อหยิบเอาแต่ละคู่ของ vertices ใน graph มาจะต้องมีเพียง 1 edge ที่เชื่อมระหว่างกันเท่านั้น ดูตัวอย่างในรูปที่ 3
♦ Connected graph หากเริ่มต้นที่ vertice ใดๆใน graph แล้ว จะสามารถเดินทางไปยัง vertices อื่นที่เหลือได้หมด (ถือเป็น complete graph แบบหนึ่ง)
♦ Cyclic graphหากนำเอา N vertices มาจาก graph แล้วพบว่ามี N edges ที่เชื่อมต่อกับ vertices เหล่านั้นแล้วเกิดเป็นวงรอบ
 |
| รูปที่ 5 ตัวอย่าง cyclic graph |
♦ Planar graph คือ graph ที่สามารถวาดให้อยู่ในรูปแบบที่ไม่มีการทับ (cross) กันของ edges
.png) |
| รูปที่ 6 |
จากรูปที่ 6 (A) อาจดูเหมือนว่าไม่ใช่ planar graph แต่ graph สามารถถูกวาดใหม่ได้หากไม่ทำให้เสียความหมาย เมื่อลองวาดใหม่จะเห็นว่าเป็น planar graph ตามรูปที่ 6 (B) ตัวอย่างนี้บอกว่าการจะบอกว่า graph ใดจะเป็น planar หรือไม่นั้นอาจใช้คำว่า "เป็นไปได้" เพราะรูปที่วาดออกมาครั้งแรกหรือถ้าโครงสร้างซับซ้อน อาจทำให้คิดว่าไม่ใช่ planar graph ก็ได้
Planar graph ทำให้เกิด face หรือ region คือพื้นที่บน plane ที่ถูกแบ่งด้วย edges จากรูปที่ 7 แสดงให้เห็น face ที่เกิดขึ้นทั้งหมด 6 faces (นับรวมพื้นที่ข้างนอก graph)
 |
| รูปที่ 7 |
ตราบใดที่ graph ที่วาดขึ้นยังเป็น planar graph ไม่ว่าจะเปลี่ยนตำแหน่งของ edges หรือ vertices ไปอย่างไร แต่จำนวน faces จะไม่เปลี่ยนแปลง
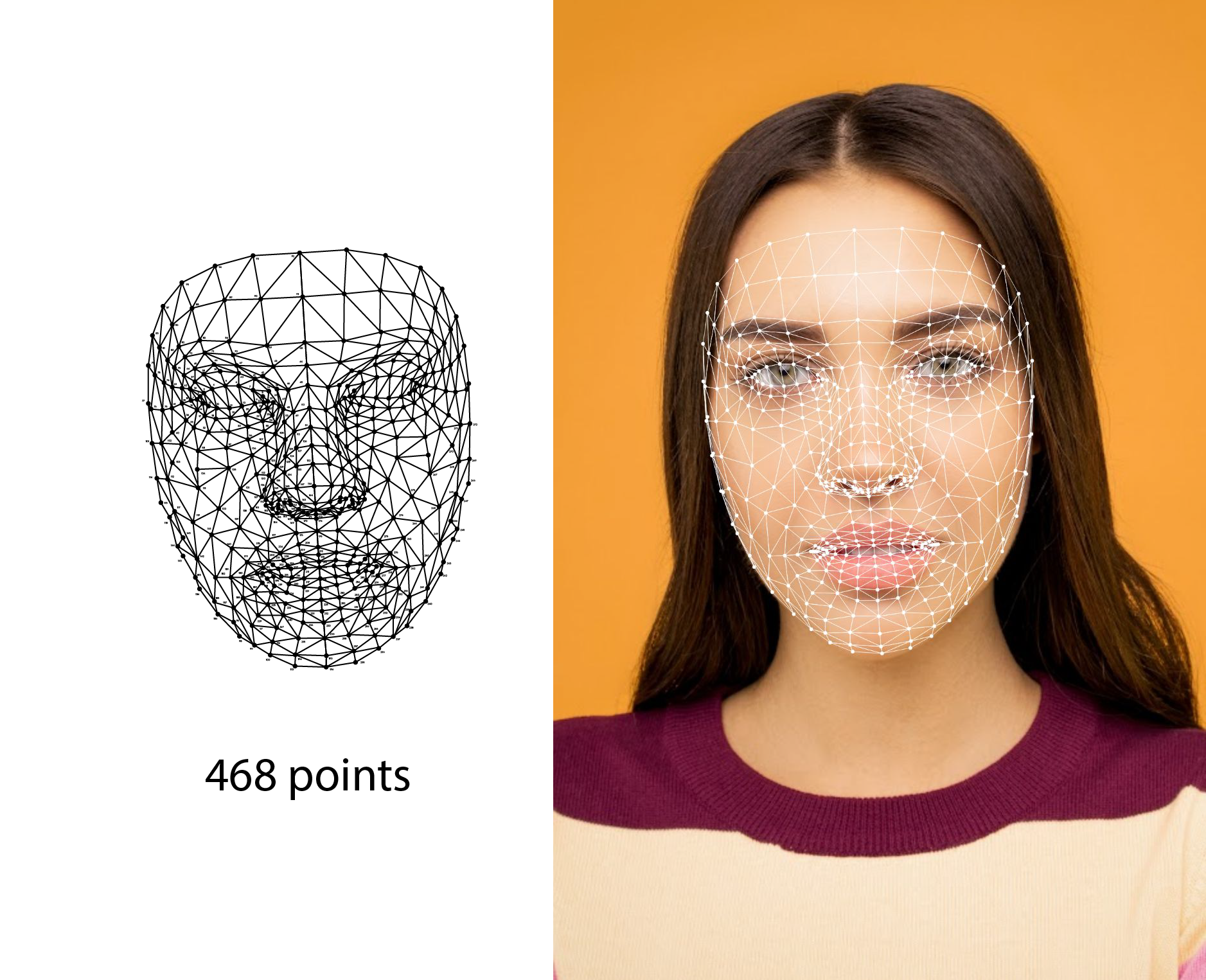 |
| รูปที่ 8 ตัวอย่าง planar graph ที่ได้จากระบบ face mesh detection |
♦Bipartite graph คือ graph ที่ vertices สามารถถูกแบ่งออกเป็น 2 กลุ่ม(set) โดยที่ vertices ที่อยู่ในกลุ่มเดียวกันจะไม่มี edges เชื่อมต่อกัน
graph G(V,E) จะเป็น bipartite graph เมื่อ
1. ถ้า V สามารถแบ่งออกเป็นสองเซต \( V_1,V_2 \) ที่ disjoint และ independent ต่อกัน
2. ทุก edges ใน E จะมีปลายด้านหนึ่งต่อกับ vertices ใน \(V_1\) และปลายอีกด้านต่อกับ vertieces ใน \(V_2\)
 |
| รูปที่ 9 ตัวอย่าง bipartite graphs |
ตัวอย่างที่ยกมาเป็นเพียงบางส่วนที่เห็นว่าได้พบกันบ่อยเท่านั้น ยังมี graph ชนิดอื่นอีก ซึ่งอาจจะได้พบในโอกาสต่อไป
Graph Representation
นอกจากการใช้ Vertices และ Edges แล้วยังมีการใช้เทคนิคอื่นที่ใช้ในการนำเสนอและเป็นตัวแบบในการจัดเก็บ graph ในหน่วยความจำคอมพิวเตอร์ ที่นิยมใช้กันได้แก่
Adjacency Matrix
เป็นการสร้าง matrix ขนาด \(n \times n \) ขึ้นมา โดย n คือจำนวน vertices สำหรับ undirected graph ถ้า vertices ในแนวตั้งและแนวนอนเชื่อมโยงกันใช้ค่า 1 ในทางตรงช้ามใช้ 0 หากใช้กับ directed graph ยังใช้ 1 และ 0 เช่นเดียวกันเพียงแต่คำนึงถึงทิศทางประกอบ
 |
| รูปที่ 10 adjacency matrix ของ undirected graph |
 |
| รูปที่ 11 adjacency matrix ของ directed graph |
 |
| รูปที่ 12 adjacency matrix ของ weighted graph |
Adjacency List
เทคนิคนี้ต้องอาศัยความรู้เรื่อง linked list ดังนั้นในตอนนี้จะกล่าวเพียงเพื่อให้รู้จักไว้เท่านั้น
 |
| รูปที่ 13 adjacency list ของ undirected graph |


ความคิดเห็น
แสดงความคิดเห็น