ในตอนที่แล้วได้กล่าวถึงขั้นตอนการคิดสำหรับคำนวณหา SVD มาแล้ว [1] มาในตอนนี้จะได้กล่าวถึงตัวอย่างการประยุกต์ใช้งานกันบ้าง โดยตอนนี้จะกล่าวถึงการนำไปช่วยลดขนาดข้อมูลของภาพลงโดยส่งผลกระทบต่อ resolution ให้น้อยที่สุด
ขั้นตอนการทำงาน
1) define function ที่จะใช้งาน
import numpy as np
import matplotlib.pyplot as plt
def SS_SVD(M):
v_val,v_vec = np.linalg.eig(M.T @ M)
i = []
temp1 = v_val.copy()
temp2 = v_val.copy()
temp1.sort()
temp1 = temp1[::-1]
for s in temp1 :
if np.round(s,4) > 0 :
i.append(np.where(temp2==s)[0])
VV = v_vec[:,i]
VV = VV.reshape((VV.shape[0],VV.shape[1]))
UU = []
for j in range(VV.shape[1]):
ui = (M @ VV[:,j])/np.sqrt(temp1[j])
UU.append(ui)
UU = np.array(UU)
UU = UU.reshape((UU.shape[0],UU.shape[1]))
return UU.T,np.diag(np.sqrt(temp1[:VV.shape[1]])),VV.T
def combine(r,g,b):
h,w = r.shape
_img = np.empty((h,w,3))
_img[:,:,0] = r
_img[:,:,1] = g
_img[:,:,2] = b
return (_img * 255).astype(np.int16)
python numpy มี module ที่ใช้หา SVD อยู่แล้วคือ numpy.linalg.svd() แต่การใช้ของตัวเองแล้วจะรู้สึกดีกว่าแม้ performance จะต่ำกว่าก็ตาม
2) นำข้อมูลภาพเข้าสู่ระบบ
img = plt.imread("michael-block-3225517.jpg")
plt.imshow(img)
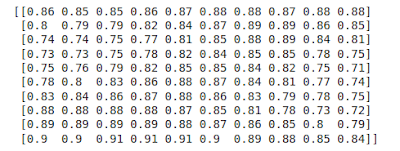
print(img[:10,:10,0]/255)
3) แยกข้อมูลออกเป็น 3 channel (R,G,B) และทำ standardize ด้วยการหารด้วย 255 ซึ่งเป็นค่าสูงสุดในระบบสี RGB colorspace เพื่อให้ค่าตัวเลขตกอยู่ระหว่าง 0.0 - 1.0
# separate color channel
red_ch = img[:,:,0].astype(np.float64)
grn_ch = img[:,:,1].astype(np.float64)
blu_ch = img[:,:,2].astype(np.float64)
# standardize
red_ch = red_ch/255.
grn_ch = grn_ch/255.
blu_ch = blu_ch/255.
4) หา SVD ของแต่ละ color channel
red_uu,red_sig,red_vt = SS_SVD(red_ch)
grn_uu,grn_sig,grn_vt = SS_SVD(grn_ch)
blu_uu,blu_sig,blu_vt = SS_SVD(blu_ch)
# preview some
print(np.round(red_uu[:10,:10],2))
print(np.round(red_sig[:10,:10],2))
print(np.round(red_vt[:10,:10],2))
มาถึงขั้นตอนนี้ จะเห็นว่า matrix ที่ได้จากภาพ ถูกแบ่งออกเป็น 3 matrix
1) matrix บนสุดเรียกว่า left singular matrix (\(U\)) มีขนาดเท่ากับ matrix ต้นฉบับ นั่นคือ แต่ละ row ของ \(U\)และต้นฉบับจะสัมพันธ์กัน
2) ถัดมาเรียกว่า singular matrix (\( \Sigma \) ) มีขนาด \( c \times c \) เมื่อ c คือจำนวน column ของ matrix ต้นฉบับ
3) ถัดมาเรียกว่า right singular matrix ( \( V^T \)) มีขนาด \( r \times r \) เมื่อ r คือจำนวน column ของ matrix ต้นฉบับ
ค่าของ singular value ระบุความสำคัญของ column vectors ที่ singular value ตัวนั้นๆอยู่ ถ้าดึงเอาแต่ singular matrix (แสดงข้อมูลบางส่วน) ออกมาพิจารณา จะเห็นว่า singular values ที่อยู่ในแนวเส้นทะแยงมุม (ในวงสีแดง) มีการเรียงลำดับจากมากไปน้อย ความหมายคือ ความสำคัญของ column vectors ใน \( U \) และ row vector ของ \(\V^T \) ถึงจัดเรียงจากซ้ายไปขวาและบนลงล่าง
มาดู correlation ระหว่าง column ใน \( U \) กันบ้าง
import pandas as pd
# using one channel is enough to see the relationship among columns
df = pd.DataFrame(data=red_uu)
corr_u = df.corr(method ='pearson')
# display some
print(corr_u.iloc[:5,:5])
#plot
plt.plot(range(350),corr_u.iloc[:,0],linewidth=2)
\[
\begin{bmatrix}
1.000000& 0.390905 &-0.020430& -0.363367& 0.218273\\
0.390905& 1.000000& 0.001301& 0.023138& -0.013899\\
-0.020430& 0.001301& 1.000000& -0.001209& 0.000726\\
-0.363367& 0.023138& -0.001209& 1.000000& 0.012920\\
0.218273& -0.013899& 0.000726& 0.012920& 1.000000\\
\end{bmatrix}
\]
จากภาพจะเห็นว่า correlation ระหว่าง column แรกของ \(U\) (ความสำคัญมากที่สุด) กับ column อื่นๆ ลดลงอย่างรวดเร็วในไม่กี่ column แรกๆ แล้วจะเข้าใกล้ 0 ไปเรื่อยๆตั้งแต่ประมาณ column ที่ 100 เป็นต้นไป แสดงว่าเราสามารถนำเอาบางส่วนของ \(U, \Sigma , V^T \) มาก็เพียงพอต่อการสร้างรูปกลับมาใหม่โดยที่สาระบนรูปยังคงใกล้เคียงของเดิมมาก ตัวอย่างในตอนนี้จะทดลองใช้ column vectors ที่แตกต่างกัน 3 ค่าคือ 150, 100 และ 25 columns ของ SVD มาสร้างรูปต้นฉบับขึ้นมาใหม่ แล้วดูความแตกต่างของภาพที่ได้ โดยอิงจากสมการ
\[ M = U\Sigma V^T \] เมื่อ
U คือ left singular matrix
V คือ right singular matrix
\( \Sigma \) คือ singular value matrix
dd=[150,100,25]
fix,axs = plt.subplots(nrows=2,ncols=2,figsize=(15,15))
axs[0,0].imshow(img)
axs[0,0].set_title("Original (450x300) , Size = {} bytes".format(img.size))
for i in range(1,4):
red_ch = red_uu[:,:dd[i-1]] @
red_sig[:dd[i-1],:dd[i-1]] @
red_vt[:dd[i-1],:]
grn_ch = grn_uu[:,:dd[i-1]] @
grn_sig[:dd[i-1],:dd[i-1]] @
grn_vt[:dd[i-1],:]
blu_ch = blu_uu[:,:dd[i-1]] @
blu_sig[:dd[i-1],:dd[i-1]] @
blu_vt[:dd[i-1],:]
req_size = 3 * (red_uu[:,:dd[i-1]].size +
red_sig[:dd[i-1],:dd[i-1]].size +
red_vt[:dd[i-1],:].size)
p = bin(i).replace('0b','')
if not len(p)>= 2:
ax = axs[0,int(p)]
else :
ax = axs[int(p[0]),int(p[1])]
ax.imshow( combine(red_ch,
grn_ch,
blu_ch))
ax.set_title("Dimension = {}, Size = {} bytes".format(dd[i-1],req_size))
จากผลลัพธ์ที่ได้ ส่วนตัวผู้เขียนเห็นว่าการลดจำนวน dimension ลงจาก 300 ไปเป็น 100 น่าจะใช้ได้ รูปที่เหมือนกับต้นฉบับมากโดยที่ใช้จำนวนข้อมูลเพียงประมาณครึ่งหนึ่งจากของเดิม ถ้าจะเปรียบเทียบให้เห็นภาพในสิ่งที่ SVD ได้ทำให้เราในการทำงานครั้งนี้ นึกภาพห้องบรรยายห้องหนึ่งมีผู้ฟัง 100 คน และมีผู้บรรยาย 4 คน บรรยายในหัวข้อเดียวกัน ต่างกันที่วิธีการใช้คำ ภาพต้นฉบับเปรียบได้กับผู้บรรยายที่ใช้จำนวนคำมาก อธิบายระเอียด เลยทำให้มีคนมีคนเข้าใจทั้งหมด 100 การลดจำนวน dimension ลงเหลือ 150 เปรียบได้กับผู้บรรยายที่ใช้คจำนวนคำน้อยลงมาหน่อย ไม่อธิบายละเอียด เลยมีผู้เข้าใจลดลง ไม่ทั้งหมด ผู้บรรยายคนถัดต่อไปมีการใช้คำน้อยลง อธิบายน้อยลง ก็เลยมีจำนวนผู้เข้าใจเนื้อหาน้อยลงตามลำดับ แต่การที่มีผู้เข้าใจน้อยลงเท่าใดจนถึงขั้นไม่น่าจะรับได้ก็ขึ้นกับผู้จัดการว่าจะเลือกเอา







ความคิดเห็น
แสดงความคิดเห็น