Singular Value Vecomposition (SVD) ขยายความจากวิธี eigendecomposition [1] ซึ่งใช้ได้กับ orthogonal matrix [3] เท่านั้น ให้สามารถ decompose matrix ที่มีขนาด \( m \times n \) ได้ด้วยสมการ
\[
M = U\Sigma A^T \tag{1}
\]
เมื่อ
M คือ matrix ขนาด \( n \times d \)
U คือ orthogonal matrix ขนาด \(n \times d \)
\(\Sigma \) คือ diagonal matrix ขนาด \( d \times d \)
A คือ orthogonal matrix ขนาด \( d \times d \)
 |
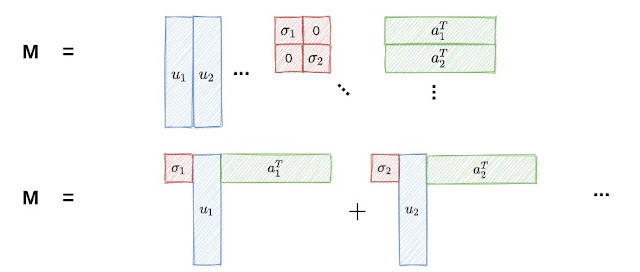| รูปที่ 1 |
รูปที่ 1 แสดงให้แนวคิดของ SVD จะเห็นว่า matrix M สามารถถูกแยก (decomposition) ออกเป็น 3 matrix ย่อย คือ U,Sigma และ A อาจมองได้ว่า element ของ M คือ span ของ dot product ระหว่าง column mantrix กับ row matrix ก็ได้
\[ M = \sum_{i=1}^{d} \sigma_i u_i a_i^T\]
ยกต้วอย่าง ถ้ามี M = \(\begin{bmatrix} 1&1&0&2\\1&1&1&2\\2&0&1&1\end{bmatrix}\) จะแยก M ออกเป็น
\[
M =
\begin{bmatrix}
0.54 & 0.71 & -0.45\\
0.54 & -0.71 & -0.45\\
0.64 & 0.00 & 0.77
\end{bmatrix} \cdot
\begin{bmatrix}
3.57 & 0.00 & 0.00\\
0.00 & 2.00 & 0.00\\
0.00 & 0.00 & 1.12
\end{bmatrix} \cdot
\begin{bmatrix}
0.66 & 0.30 & 0.48 & 0.48\\
0.00 & 0.00 & -0.71 & 0.71\\
0.00 &-0.81 &-0.13 &-0.13
\end{bmatrix}
\]
ลองคำนวณแยกกัน
\[
\begin{align*}
C_1 &= 3.57
\begin{bmatrix}
0.54\\
0.54\\
0.64
\end{bmatrix} \cdot
\begin{bmatrix}
0.66 & 0.30 & 0.48 & 0.48
\end{bmatrix} \\\\
&=
\begin{bmatrix}
1.28& 0.59& 0.94& 0.94\\
1.28& 0.59& 0.94& 0.94\\
1.52& 0.7 & 1.11& 1.11
\end{bmatrix}\\\\
C_2 &= 2.00
\begin{bmatrix}
-0.45\\
-0.45\\
0.77
\end{bmatrix} \cdot
\begin{bmatrix}
0.00 & 0.00 & -0.71 & 0.71\\
\end{bmatrix} \\\\
&=
\begin{bmatrix}
0. & 0.& -1.& 1.\\
0. & 0.& 1.& -1.\\
0. & 0.& 0.& 0.
\end{bmatrix} \\\\
C_3 &= 1.12
\begin{bmatrix}
0.71\\
-0.71\\
0.00
\end{bmatrix} \cdot
\begin{bmatrix}
0.56 &-0.81& -0.13 & -0.13\\
\end{bmatrix} \\\\
&=
\begin{bmatrix}
-0.28 & 0.41 & 0.06& 0.06\\
-0.28 & 0.41& 0.06 & 0.06\\
0.48 &-0.7& -0.11 &-0.11\\
\end{bmatrix} \\\\
\therefore C_1 + C_2 +C_3 &= M
\end{align*}
\]
ก่อนที่จะเข้าเนื้อหาของที่มาของสมการ (1) มาทำความรู้จักกับ singular values กันก่อน
ถ้า M เป็น matrix ขนาด \( n \times d \) และกำหนดให้ \( \lambda_1,\lambda_2,\lambda_3,...,\lambda_d \) เป็น Eigen values ของ \( M^T \cdot M \) โดย \( \lambda_1 \geq \lambda_2 \geq \lambda_3 ... \geq \lambda_d \geq 0 \) และ \( \sigma_1 = \sqrt{\lambda_1},\sigma_2 = \sqrt{\lambda_2}, \sigma_3 = \sqrt{\lambda_3},..., \sigma_d = \sqrt{\lambda_d} \) เรียก \(\sigma_1,\sigma_2,\sigma_3,...,\sigma_d \) ว่า "singular values" ของ A
การคำนวณ SVD
เพื่อให้เข้าใจที่มาของสมการ (1) จะเริ่มด้วยทบทวนการ decompose vector ในระบบ \( R^2 \) ก่อน
 |
| รูปที่ 2 |
ในรูปที่ 2 \(\vec{v} \) ถูกแยก (decomposed) ออกเป็น \(\vec{v}_x \) และ \(\vec{v}_y \) ซึ่งเป็น projection บนแกน x,y ตามลำดับ
\[ \vec{v} = \vec{v}_x + \vec{v}_y \]
และกำหนดให้
\( \vec{a}_x = \begin{bmatrix}1\\0 \end{bmatrix} \) และ \( \vec{a}_y = \begin{bmatrix}0\\1 \end{bmatrix}\) เป็น unit vector บนแกน x และ y (basis) ตามลำดับ
\( \theta \) คือมุมระหว่าง \(\vec{v} \) กับแกน x \( \gamma \) คือมุมระหว่าง \(\vec{v} \) กับแกน y
จะได้ว่า
\[
\begin{align*}
\vec{v} \cdot \vec{a}_x &= \|\vec{v} \| \|\vec{a}_x \| cos \theta \\\\
&= \|\vec{v} \| \frac{\|\vec{v}_x \|}{\|\vec{v} \|} \\\\
\vec{v} \cdot \vec{a}_x &= \|\vec{v}_x \| = S_x \tag{2}
\end{align*}
\]
ทำนองเดียวกัน
\[
\begin{align*}
\vec{v} \cdot \vec{a}_y &= \|\vec{v} \| \|\vec{a}_y \| cos \gamma \\\\
&= \|\vec{v} \| \frac{\|\vec{v}_y \|}{\|\vec{v} \|} \\\\
\vec{v} \cdot \vec{a}_y &= \|\vec{v}_y \| = S_y \tag{3}
\end{align*}
\]
หมายเหตุ \( \| \vec{a}_x \| = 1,\| \vec{a}_y \| = 1\)
หากกรณีที่มี vector จำนวนมาก และอยู่ในระบบที่มี basis เป็น \( \begin{bmatrix} a_1^x \\ a_2^x \end{bmatrix} \) และ \( \begin{bmatrix} a_1^y \\ a_2^y \end{bmatrix} \) (ดูเรื่อง การย้าย basis of vector ใน [6] ประกอบ) แสดงในรูปที่ 3(a)-(b)
 |
| รูปที่ 3 |
อ้างอิงจากสมการ (2),(3) พิจารณาที่ \( \vec{v}_1\)
\[
\begin{align*}
\vec{v}_1 \cdot \vec{a}^x &= S_1^x \\
\vec{v}_1 \cdot \vec{a}^y &= S_1^y \\\\
\begin{bmatrix}v_1^x\\v_1^y \end{bmatrix} \cdot \begin{bmatrix} a_1^x\\a_2^x\end{bmatrix} &= S_1^x \tag{4} \\\\
\begin{bmatrix}v_1^x\\v_1^y \end{bmatrix} \cdot \begin{bmatrix} a_1^y\\a_2^y\end{bmatrix} &= S_1^y \tag{5} \\\\
\end{align*}
\]
สมการ (4),(5) สามารถถูกรวมเข้าด้วยกัน แล้วเขียนในรูปแบบของ matrix - vector multiplication ได้
\[
\begin{bmatrix}v_1^x & v_1^y \end{bmatrix} \cdot
\begin{bmatrix} a_1^x & a_2^x \\ a_1^y & a_2^y \end{bmatrix}
=
\begin{bmatrix}S_1^x & S_1^y \end{bmatrix} \tag{6}
\]
ถ้า \(\vec{v}_2 = \begin{bmatrix}v_2^x\\v_2^y \end{bmatrix} \) ถูกเพิ่มเข้าไปในระบบ สมการที่ (6) จะเปลี่ยนเป็น
\[
\begin{bmatrix}v_1^x & v_1^y \\ v_2^x & v_2^y \end{bmatrix} \cdot
\begin{bmatrix} a_1^x & a_2^x \\ a_1^y & a_2^y \end{bmatrix}
=
\begin{bmatrix}S_1^x & S_1^y\\S_2^x & S_2^y \end{bmatrix} \tag{7}
\]
พิจารณาสมการ (6)และ (7) ถ้ามีการเพิ่ม vector เข้าไปเรื่อย ๆ รูปแบบทั่วไปของสมการที่ (7) จะกลายเป็น
\[
\begin{bmatrix}
v_1^x & v_1^y \\
v_2^x & v_2^y \\
\vdots & \vdots
\end{bmatrix}
\cdot
\begin{bmatrix} a_1^x & a_2^x \\ a_1^y & a_2^y \end{bmatrix}
=
\begin{bmatrix}
S_1^x & S_1^y\\
S_2^x & S_2^y \\
\vdots & \vdots
\end{bmatrix}
\tag{8}
\]
เขียนสมการ (8) ในรูปแบบอย่างง่ายคือ
\[
V \cdot A = S \tag{9}
\]
ถ้าให้ d = จำนวน dimension (axis) ข้อมูล และ n = จำนวน data points หรือ จำนวน vectors จะได้ขนาดของ matrix ในสมการ (9) ดังนี้
V เป็น rectangle matrix ขนาด \( n \times d\)
A เป็น square matrix ขนาด \( d \times d\)
S เป็น rectangle matrix ขนาด \( n \times d\)
พิจารณา matrix A ในสมการ (9) จะเห็นว่า row vector คือ unit vector ที่อยู่บน axis แต่ละ axis ซึ่งจะตั้งฉากต่อกันทุก axis นั่นคือ matrix A เป็น orthogonal matrix [7] นั่นคือ \( A^{-1} = A^T \) อาศัยคุณสมบัตินี้ จะเขียนสมการ (9) ใหม่ได้เป็น
\[
\begin{align*}
V \cdot A &= S \\
V \cdot A \cdot A^{-1} &= S \cdot A^T \\
V &= S \cdot A^T \tag{10}
\end{align*}
\]
มาถึงขั้นตอนนี้ จะเริ่มเห็นได้ว่าสมการ (10) มีลักษณะคล้ายกับสมการ (1) แต่ยังไม่เหมือนทีเดียว ตัวที่ขาดไปคือ U และ \( \Sigma \)
มาพิจารณาดู S , elements ในแต่ละ column vectors ของ S คือค่าของ norm ของ projected vectors บนแต่ละ axis
\[
\begin{bmatrix}
S_1^x & S_1^y & \cdots \\
S_2^x & S_2^y & \cdots \\
\vdots & \vdots & \vdots
\end{bmatrix}
\]
หากต้องการทำให้แต่ละ column vector อยู่ในรูปของ unit vector ก็เพียงแต่หารแต่ละ column vector ด้วย norm ของแต่ละ column vector เอง
\[
\begin{align*}
\begin{bmatrix}
\frac{S_1^x}{\sigma_1} &
\frac{S_1^y}{\sigma_2} & \cdots \\
\frac{S_2^x}{\sigma_1} &
\frac{S_2^y}{\sigma_2} & \cdots \\
\vdots & \vdots & \vdots
\end{bmatrix}
\end{align*}
\]
เขียนให้อยู่ในรูปแบบอย่างง่ายเป็น \[ S = U \cdot \Sigma \] เมื่อ U เป็น orthogonal matrix (column vectors ตั้งฉากต่อกัน) ขนาด \( n \times d \) และ \( \Sigma \) เป็น diagonal matrix ขนาด \( d \times d \) นำเอา \( U , \Sigma \) ไปแทน S ใน (10) จะได้
เมื่อ \( \sigma_n \) คือ norm ของ column vector ที่ n นั่นคือ S จะถูกแยกออก
\[ \begin{align*} \begin{bmatrix} S_1^x & S_1^y & \cdots \\ S_2^x & S_2^y & \cdots \\ \vdots & \vdots & \vdots \end{bmatrix} &= \begin{bmatrix} \frac{S_1^x}{\sigma_1} & \frac{S_1^y}{\sigma_2} & \cdots \\ \frac{S_2^x}{\sigma_1} & \frac{S_2^y}{\sigma_2} & \cdots \\ \vdots & \vdots & \vdots \end{bmatrix} \cdot \begin{bmatrix} \sigma_1 & 0 & \cdots \\ 0 & \sigma_2 & \cdots \\ \vdots & \vdots & \sigma_n \end{bmatrix}\\\\ \end{align*} \]หมายเหตุ \( \sigma \) ไม่จำเป็นต้องใช้ norm ของ column vector การใช้ค่าคงที่อื่นจะได้ผลเช่นเดียวกัน ค่าที่นิยมใช้คือ Eigen value (\( \lambda \) )โดย \(\sigma^2 = \lambda \)
เขียนให้อยู่ในรูปแบบอย่างง่ายเป็น \[ S = U \cdot \Sigma \] เมื่อ U เป็น orthogonal matrix (column vectors ตั้งฉากต่อกัน) ขนาด \( n \times d \) และ \( \Sigma \) เป็น diagonal matrix ขนาด \( d \times d \) นำเอา \( U , \Sigma \) ไปแทน S ใน (10) จะได้
\[
V = U \Sigma A^T \tag{11}
\]
เนื่องจาก A เป็น orthogonal matrix เราจึงอาจได้เห็นการเขียนสมการที่ (11) ในอีกรูปแบบคือ
\[
V = U \Sigma A^{-1} \tag{12}
\]
การคำนวณหา A ในสมการ (11),(12) จาก
\[
V = U \Sigma A^T \\
\]
dot product ด้วย \(V^T \)
\[
\begin{align*}
V^T \cdot V &= V^T \cdot (U \Sigma A^T) \\
V^T \cdot V &= (U \Sigma A^T)^T \cdot (U \Sigma A^T) \\
V^T \cdot V &= (A^T)^T \Sigma^T U^T U \Sigma A^T\\
V^T \cdot V &= A \Sigma \Sigma A^T \\
V^T \cdot V &= A \Sigma^2 A^T \\
\end{align*}
\]
dot product ด้วย A
\[
\begin{align*}
V^T \cdot V \cdot A &= A \Sigma^2 A^T A \\
V^T \cdot V \cdot A &= A \Sigma^2 \tag{13}\\
\end{align*}
\]
พิจารณาสมการ (13) จะเห็นว่ามีรูปแบบเดียวกับการหา Eigen value / Eigen vector เทียบเคียงดังนี้
1. \( V^T V \) เป็น square matrix
2. A คือ matrix ที่มี column vectors คือ Eigen vectors ของ \( V^T V \)
3. \( \Sigma^2 \) เป็น diagonal matrix ที่สร้างจาก Eigen values ของ \( V^T V\)
\[
\begin{align*}
\Sigma^2 &=
\begin{bmatrix}
\sigma_1^2 & 0 & 0 & \cdots \\
0 & \sigma_2^2 & 0 & \cdots \\
0 & 0 & \sigma_3^2 & \cdots \\
\vdots & \vdots & \vdots & \sigma_n^2 \\
\end{bmatrix}
=
\begin{bmatrix}
\lambda_1 & 0 & 0 & \cdots \\
0 & \lambda_2 & 0 & \cdots \\
0 & 0 & \lambda_3 & \cdots \\
\vdots & \vdots & \vdots & \lambda_n \\
\end{bmatrix}
\end{align*}
\]
โดย \( \lambda_i = \sigma_i^2 \) เมื่อกลับไปพิจารณานิยามของ singular values ที่กล่าวไว้แล้วข้างต้น \( Sigma \) คือ matrix ของ singular values ของ \( V \) นั่นเอง
กล่าวโดยสรุปคือ
1) A หาได้จาก Eigen vector ของ \(V^TV \)
2) \( \Sigma \) สร้างจาก Eigen values ของ \(V^TV \)
การหา U ในสมการ (11),(12)
จาก
\[
V = U \Sigma A^T \\
\]
dot product ด้วย A ทั้งสองข้าง
\[
\begin{align*}
V A &= (U \Sigma A^T) A \\
&= U \Sigma \\
\end{align*}
\]
dot product ด้วย \( \Sigma^{-1}\)ทั้งสองข้าง
\[
\begin{align*}
VA\Sigma^{-1} &= U \Sigma \Sigma^{-1} \\
U &= VA\Sigma^{-1} \tag{14}
\end{align*}
\]
A และ \( \Sigma \) หาได้จากวิธีการที่กล่าวมาแล้วในสมการ (13) และเนื่องจาก \( \Sigma \) เป็น orthogonal matrix ดังนั้น \(\Sigma^{-1} =
\begin{bmatrix}
\frac{1}{\sigma_1} & 0 & 0 & ... \\
0 & \frac{1}{\sigma_2} & 0 & ... \\
0 & 0 & \frac{1}{\sigma_3} & ... \\
\vdots & \vdots & \vdots & \frac{1}{\sigma_n}
\end{bmatrix}\)
SVD นับว่าเป็นพื้นฐานสำคัญอันหนึ่งของ linear algebra ถูกนำไปใช้งานหลายด้านโดยเฉพาะ unsupervised machine learning ตัวอย่างที่มักถูกอ้างถึงบ่อยคือ Principle Componenet Analysis (PCA), ลดขนาดของภาพ, ระบบแนะนำสินค้าสมาชิก ฯลฯ ตัวอย่างการประยุกต์จะของกล่าวถึงในตอนต่อไป แต่ในตอนนี้ขอจบด้วย python code ที่เป็นการสรุปเนื้อหาที่กล่าวถึงในตอนนี้ดังนี้
import numpy as np
def SS_SVD(M):
# construct square matrix (covariance matrix of itself)
v_val,v_vec = np.linalg.eig(M.T @ M)
# to store right singular matrix indecies
i = []
temp1 = v_val.copy()
temp2 = v_val.copy()
# singular values need to be sorted.
temp1.sort()
temp1 = temp1[::-1]
for s in temp1 :
# to include only more than zero elements
if np.round(s,4) > 0 :
i.append(np.where(temp2==s)[0])
# construct right singular matrix
VV = v_vec[:,i]
VV = VV.reshape((VV.shape[0],VV.shape[1]))
# construct left singular matrix
UU = []
for j in range(VV.shape[1]):
ui = (M @ VV[:,j])/np.sqrt(temp1[j])
UU.append(ui)
UU = np.array(UU)
UU = UU.reshape((UU.shape[0],UU.shape[1]))
# construct sigular matrix
singular_mat = np.diag(np.sqrt(temp1[:VV.shape[1]]))
return UU.T,singular_mat,VV.T
เอกสารอ้างอิง
[1] https://smarter-machine.blogspot.com/2021/03/basic-linear-algebra-eigendecomposition.html
[2] https://en.wikipedia.org/wiki/Singular_value_decomposition
[3] https://smarter-machine.blogspot.com/2021/03/basic-linear-algebra-orthogonal-matrix.html
[4] https://smarter-machine.blogspot.com/2021/02/basic-linear-algebra-vector-part.html#dot_pro
[5] https://smarter-machine.blogspot.com/2021/03/basic-linear-algebra-eigendecomposition.html
[6] https://smarter-machine.blogspot.com/2021/03/basic-linear-algebra-basis-of-vector.html
[7] https://smarter-machine.blogspot.com/2021/03/basic-linear-algebra-orthogonal-matrix.html
ความคิดเห็น
แสดงความคิดเห็น