Counting Principle part 3 : Permutation และ Combination

• Part 1
• Part 2

Permutation

ถ้าให้เลือกจักรยานยนต์มา 2 คันจาก 4 คัน การหาทางเลือกที่เป็นไปได้ทั้งหมดโดยใช้แผนภาพต้นไม้(tree diagram) จะได้ทางเลือกทั้งหมด 12 ทางเลือก (ภาพที่ 1)

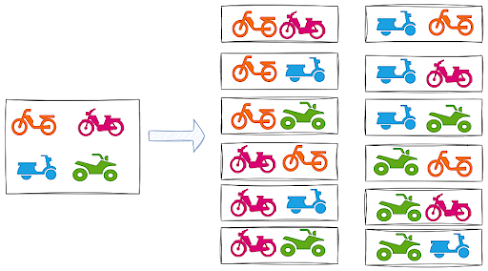ภาพที่ 1

หากต้องการใช้การคำนวณแทนการวาดแผนภาพ ก็สามารถใช้แยกเป็นงานย่อย 2 งานที่ทำต่อเนื่องกันคือ

1. เลือกรถคันแรก จะมีทางเลือก 4 ทางลือกเท่ากับจำนวนรถที่มี เพราะยังไม่ได้ถูกเลือกมาก่อน
2. เลือกรถคันที่สอง เนื่องจากถูกเลือกไปจากงานแรกแล้ว 1 คัน จำนวนรถที่เลือกได้จะเหลือ 3 คัน

ตามหลักการของ multiplication principle แล้ว จำนวนทางเลือกทั้งหมดคือ \( 4 \times 3 = 12 \text{ ทางเลือก} \)

จากภาพที่ 1 จะเห็นว่าการเลือกรถออกมาจากกลุ่มเดิมดูเหมือนกับการสร้างกลุ่มย่อย (subset) ขึ้นมาภายใต้เงื่อนไขที่กำหนด กลุ่มย่อยที่อาจมีสมาชิกที่เหมือนกันแต่ถ้าการจัดเรียงที่ต่างกันก็นับว่าเป็นคนละกลุ่มย่อยกัน การหารูปแบบทั้งหมดของกลุ่มย่อยแล้วทำการนับจำนวน (แจงแล้วนับ) ทางคณิตศาสตร์เรียกว่า "Permutation"

สัญญลักษณ์ที่ใช้แทน Permutation มีหลายรูปแบบ เช่น \( _nP_k\),\(P_{n,k}\),\(P(n,k)\),\(P^n_k\) โดย n แทนจำนวนสิ่งของที่มีอยู่ และ k แทนจำนวนสิ่งที่ถูกเลือก โดยมีสูตรการคำนวณดังนี้

\[ P(n,k) = \frac{n!}{(n-k)!} \tag{1.0}\]

\(n! \) อ่านว่า n-factorial เมื่อ n เป็นจำนวนเต็มบวกและไม่เท่ากับศูนย์ โดย \[n! = n \times (n-1) \times (n-2) \times ... \times 1 \tag{2.0}\] และกำหนดให้ \( 0! \text{ และ } 1! = 1 \)

เช่น

• \( 2! = 2 \times 1 \)
• \( 5! = 5 \times 4 \times 3 \times 2 \times 1 \)
• \( 10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \)

ตัวอย่าง

1. ถ้ามีหนังสือที่ต่างกัน 7 เล่ม จะมีวิธีการจัดเรียงหนังสือบนชั้นวางหนังสือได้กี่วิธี

การคำนวณในข้อนี้ ยังไม่ต้องใช้สูตร (1.0) เพราะไม่ได้ระบุจำนวนของหนังสือที่ต้องเลือกออกมา ก็สรุปว่าต้องการเรียงหนังสือทั่ง 7 เล่ม ซึ่งการมองว่าเป็นงานที่ทำต่อเนื่องกัน 7 งานแต่ละงานคือการหยิบหนังสือขึ้นไปวางบนชั้นจะเห็นภาพที่ชัดเจนกว่า

งานที่ 1 มีทางเลือก 7 ทางเลือก

งานที่ 2 มีทางเลือก 6 ทางเลือก

งานที่ 3 มีทางเลือก 5 ทางเลือก

งานที่ 4 มีทางเลือก 4 ทางเลือก

งานที่ 5 มีทางเลือก 3 ทางเลือก

งานที่ 6 มีทางเลือก 2 ทางเลือก

งานที่ 7 มีทางเลือก 1 ทางเลือก

\( \therefore \) ตาม Multiplication principle ทางเลือกทั้งหมดจะเป็น \(7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 7!\)

ลองนำกรณีนี้ไปใช้กับสูตร (1.0) เนื่องจากต้องการนำหนังสือทุกเล่มไปจ้ดวาง ดังนั้นจะได้ว่า n = 7 และ k = 7 หรือ \( P(7,7) \) นำไปแทนใน (1.0)

\[ \begin{align*} P(7,7) &= \frac{7!}{(7-7)!} \\ &= \frac{7!}{0!} \\ &= 7! \end{align*} \]

จากตัวอย่าง ทำให้ทราบว่า

\[ P(n,n) = n! \tag{3.0} \]

อาจกล่าวได้ว่า หากเรามี finite set ที่มีสมาชิก n แล้ว permutation ของเซตนั้นคือ n!

2. จะมีวิธีจัดให้นักเดินทาง 4 คนเดินทางโดยพาหนะต่างกัน 3 ชนิดได้กี่วิธี โดยกำหนดให้พาหนะแต่ละชนิดรับนักเดินทางได้ 1 คน

ข้อนี้สามารถใช้สูตร (1.0) ได้ โดย n = 4, k=3

\[ \begin{align*} P(4,3) &= \frac{4!}{(4-3)!} \\ &= \frac{4!}{1!} \\ &= 4! \\ &= 24 \\ \end{align*} \]

Combination

กลับไปพิจารณาภาพที่ 1 เราทราบแล้วว่า Permutation คือ \(\frac{4!}{(4-2)!} \) หากใช้มุมมองเรื่องเซตมาใช้คำนวณ เราจะได้วิธีการคำนวณอีกวิธีหนึ่งดังนี้

1. กำหนดให้ C แทนจำนวนเซตที่มีสมาชิกเป็นรถจักรยานยนต์ 2 คัน ตามที่กำหนดไว้

2. ความรู้จากสมการ (3.0) Permutation ของแต่ละเซตที่กำหนดไว้ในข้อ 1 จะเป็น 2!

3. ดังนั้นจำนวนวิธีที่จะจัดเรียงสมาชิกของเซตจำนวน C เซต จะเป็น \( C \times 2! \)

4. ค่าที่คำนวณได้ในข้อ 3 ต้องเท่ากับ \(\frac{4!}{(4-2)!} \) เพราะเรากำลังคำนวญหาสิ่งเดียวกัน แต่คนละวิธีคิด ดังนั้น \[ \begin{align*} P(4,2) &= C \times 2! \\ \frac{4!}{(4-2)!} &= C \times 2! \\ \therefore C &= \frac{1}{2!} \times \frac{4!}{(4-2)!} \tag{4.0} \\ \text{หรือ} \\ C &= \frac{P(n,k)}{k!},n=4,k=2 \tag{4.1}\\ \end{align*} \]

ค่าของ C ที่คำนวณได้ เรียกว่าค่า Combination ซึ่งก็คือจำนวนของ subset ที่จะสามารถสร้างได้เมื่อเลือกสมาชิกจำนวน k จากเซตที่มีสมาชิก n นั่นเอง

สัญญลักษณ์ที่ใช้เขียนแทน Combination มีหลายแบบ เช่น \(^nC_k , C(n,k),_nC_k, \begin{pmatrix} n\\k\end{pmatrix}\) โดยมีสูตรคำนวณดังนี้

\[ C(n,k) = \frac{n!}{k!(n-k)!} \tag{5.0}\]

ตัวอย่าง

1. ร้านขายโยเกิร์ต มี topping ให้ลูกค้าได้เลือก 10 ชนิด โดยลูกค้าสามารถเลือกได้ 3 ชนิดต่อโยเกิร์ต 1 ถ้วย (ห้ามเลือกซ้ำ) ร้านนี้จะสามารถสร้างรายการ topping ที่แตกต่างกันได้กี่รายการ

การเลือก Topping จะเป็นรูปแบบของ combination เพราะลำดับของการเลือกไม่มีผลต่อรายการ ข้อนี้สามารถคำนวณโดยใช้ (5.0) ได้ \[ \begin{align*} C(10,3) &= \frac{10!}{3!(10-3)!} \\ &= \frac{10!}{3!7!}\\ &= \frac{10 \times 9 \times 8 \times 7!}{3 \times 2 \times 7!} \\ &= \frac{10 \times 9 \times 8 }{3 \times 2} \\ &=120 \end{align*} \]

Binomial Coefficients

อ้างอิงจาก Binomial theorem

\[ (x +y)^n = \sum_{j=0}^n \begin{pmatrix} n\\j \end{pmatrix} x^{n-j}y^j \tag{6.0}\]

สังเกตุดูจะเห็นว่าสูตรที่ใช้คำนวณหาค่า combination ถูกนำไปใช้ในการหา coefficient ของ binomial ด้วย

ตัวอย่าง

1. \( (2x+3y)^3 = ? \)

\[ \begin{align*} (2x+3y)^3 &= \sum_{j=0}^3 \begin{pmatrix} 3\\j \end{pmatrix} (2x)^{3-j}(3y)^j \\ &= \begin{pmatrix} 3\\0 \end{pmatrix} (2x)^{3-0}(3y)^0 + \begin{pmatrix} 3\\1 \end{pmatrix} (2x)^{3-1}(3y)^1 + \begin{pmatrix} 3\\2 \end{pmatrix} (2x)^{3-2}(3y)^2 + \begin{pmatrix} 3\\3 \end{pmatrix} (2x)^{3-3}(3y)^3 \\ &= (2x)^3 + 3(2x)^2(3y) + 3(2x)(3y)^2 +(3y)^3\\ &= 8x^3+36x^2y + 54xy^2+27y^3 \end{align*} \]

Permutation คือการหาจำนวนของทางเลือกในการจัดเรียงสิ่งของ (finding the number of ways of arrange a certain number of distinct elements)

Combination คือการหาจำนวนของทางเลือกในการเลือกสิ่งของ (finding the number of ways of selecting a certain number of distinct elements)

ขอให้สังเกตุว่ามีการใช้คำ "distinct elements" ซึ่งเป็นคุณสมบัติพื้นฐานของสมาชิกในเซต ดังนั้นจำเป็นต้องให้มั่นใจว่าสิ่งของที่จะมาหา Permutation หรือ Combination ต้องมากจาก distinct elements

แบบฝึกหัด

1. กำหนดชุดอักษร ABCDEFG จงคำนวณหา Permutation ของการนำตัวอักษรทุกตัวในชุดที่กำหนดให้มาจัดเรียงใหม่โดยไม่สนใจความหมายของคำ

    1.1 มีเงื่อนไขว่าทุกคำที่สร้างขึ้นมาต้องเริ่มต้นด้วย ABC

ABCDEFG มีอักษรทั้งหมด 7 ตัว โจทย์กำหนดว่าทุกคำที่สร้างขึ้นต้องขึ้นต้นด้วย ABC นั่นคือการกำหนดตำแหน่งที่ตายตัว ดังนั้นต้องสร้างคำจากอักษร 4 ตัวที่เหลือ จาก \(P(n,n) = n! \) \[ \begin{align*} P(4,4) &= 4! \\ P(4,4) &= 24 \\ \end{align*} \]

    1.2 มีเงื่อนไขว่าทุกคำที่สร้างขึ้นมาต้องมีชุดตัวอักษร ABC

เงื่อนไขข้อนี้ต่างจาก 1.1 คือไม่ได้กำหนดตำแหน่งของชุดอักษร ABC จึงต้องมองว่า ABC เปรียบเหมือนตัวอักษร 1 ดังนั้นต้องสร้างคำจากอักษร 5 ตัว \[ \begin{align*} P(5,5) &= 5! \\ P(5,5) &= 120 \\ \end{align*} \]

2. คำนวณหา Permutation จากคำ "BANGKOK"

"BANGKOK" ประกอบด้วยตัวอักษร 7 ตัว Permutation คือ \[ \begin{align*} P(7,7) &= 7! \\ \end{align*} \]

แต่เมื่อพิจารณาดูจะเห็นว่า K มีซ้ำกัน 2 ตัว ซึ่งไม่ใช่ distinct elements ดังนั้นจำเป็นต้องนำเอาส่วนที่เกิดจากการซ้ำออกไปด้วยการหารออกนั่นคือ \( P(2,2) = 2!\)

คำตอบที่ถูกต้องจึงเป็น \[ \begin{align*} \text{Permutation} &= \frac{7!}{2!}\\ &= 2520 \end{align*} \]

3. คนจำนวน 20 คน ถ้าให้แต่ละคนจับมือทักทายกับคนอื่นที่เหลือ จงคำนวณว่าการจับมือจะเกิดขึ้นทั้งหมดกี่ครั้ง

วิธีที่ 1 :

แต่ละคนจะต้องจับมือทั้งหมด 19 ครั้ง (การจับมือกับตัวเอง ไม่เกิดขึ้น) ดังนั้นคน 20 คนจะต้องจับมือทั้งหมด \( 20 \times 19 = 380 \) ครั้ง แต่ในทางปฏิบัติการนับแบบนี้จะรวมเอาการจับที่ซ้ำ เข้าไปด้วย เช่น A จับมือกับ B และ B จับมือกับ A จะถือว่าเป็นการจับมือเพียงครั้งเดียว ดังนั้นจำนวนครั้งของการจับมือที่ตัดเอาการจับมือซ้ำออกไปจะเป็น \( \frac{380}{2} = 190 \) ครัง

วิธีที่ 2 :

ใช้ Combination โดยพิจารณาเหมือนกับการเลือกคน 2 คนจาก 20 คนมาจับมือกัน จะได้ทั้งหมดกี่วิธี

\[ \begin{align*} C(20,2) &= \frac{20!}{2!(20-2)!}\\ &= \frac{20!}{2! 18!}\\ &= 190\\ \end{align*} \]