Probability : Naive Bayes classifier ภาคทฤษฎี

แนวคิด (Basic idea)

เป้าหมายของ Bayes classifier คือการประมาณค่าความน่าจะเป็นของเหตการณ์ y ภายใต้เงื่อนไขการเกิดขึ้นของเหตุการณ์ x จากเรื่อง conditional probability เราทราบว่า

\[ \begin{align*} p(y \mid x) &= \frac{p(y \cap x)}{p(x)} \tag{1.0} \\ \\ p(y \mid x) &= \frac{p(y) p(x \mid y) }{p(x)} \tag{1.1} \\ \end{align*} \]

ตัวอย่างข้อมูลของสายพันธุ์ดอก Iris (รูปที่ 1)  

รูปที่ 1 ตัวอย่างข้อมูลการแบ่งกลุ่มดอก Iris

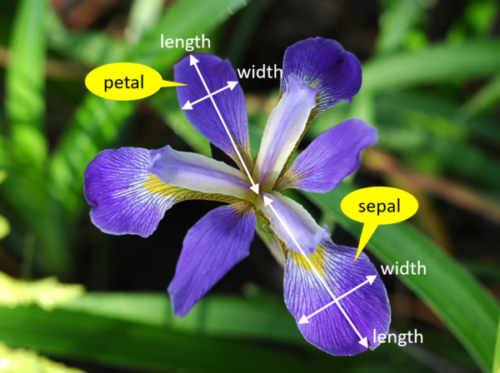รูปที่ 2 คุณลักษณะของดอก Iris ที่นำไปใช้ในการแบ่งสายพันธุ์

ถ้าให้ y แทนเหตุการณ์ที่ข้อมูลในแต่ละแถวจะเป็นสายพันธุ์ (class) ของดอก ค่าที่เป็นไปได้ของ  y คือ  ["setosa", "vericolor" , "verginica" ]

\( x_1 \) แทนเหตุการณ์ของ sepal length ที่วัดได้

\( x_2 \) แทนเหตุการณ์ของ sepal width ที่วัดได้

\( x_3 \) แทนเหตุการณ์ของ petal length ที่วัดได้

\( x_4 \) แทนเหตุการณ์ของ petal width วัดได้

จะเห็นว่าค่าของ y จะเป็นค่าใดขึ้นกับค่าของ \( x_1,x_2,x_3,x_4 \) ที่เกิดขึ้น เช่น  
  • ถ้า \( x_1 = 5.1, x_2 = 3.5, x_3 = 1.4, x_4 = 0.2 \) แล้ว y เป็น 'setosa' หรือ 
  • ถ้า \( x_1 = 6.7, x_2 = 3.0, x_3 = 5.2, x_4 = 2.3 \) แล้ว y เป็น 'verginica' 

สามารถเขียนความสัมพันธุ์ระหว่าง \( x_1,x_2,x_3,x_4 \) กับ y ตามแบบ conditional probability ได้ดังนี้

\[ \begin{align*} p( y =\text{sentosa} \mid x_1 = 5.1, x_2 = 3.5,x_3=1.4 ,x_4 = 0.2) \approx 1.0 \\ p( y =\text{verginica} \mid x_1 = 6.7, x_2 = 3.0, x_3 = 5.2, x_4 = 2.3) \approx 1.0 \\ \end{align*} \]

หมายความว่า ถ้าเราทราบการแจกแจงค่าความน่าจะเป็นของ \( x_1,x_2,x_3,x_4 \)  ของ Iris แต่ละสายพันธุ์แล้ว ภายหลังเมื่อเราได้ข้อมูลใหม่เข้ามาในรูปของ \( x_1,x_2,x_3,x_4 \) แล้ว เราจะสามารถพยากรณ์ได้ว่า ข้อมูลชิ้นนั้นเป็นของ Iris สายพันธุ์ใดได้ (คือการหาค่าใน (1.0) หรือ (1.1) )

หมายเหตุ เราอาจเขียน (\( x_1,x_2,x_3,x_4 \)) ในรูปของ \( \vec{x} \) แทนได้ 

จาก (1.1) เป็นการประมาณค่าความน่าจะเป็นของ y เมื่อทราบเงื่อนไข \( \vec{x} \)  

\[ P(y \mid \vec{x}) = \frac{P(y) \cdot P(\vec{x} \mid y)}{P(\vec{x})} \tag{1.2} \]

ในทางปฏิบ้ติมีข้อคำนึงอยู่คือ

  1. เราสามารถหาค่าของ \(P(y) \) ได้โดยการแจงนับจากข้อมูลตัวอย่างที่เก็บมา
  2. \( P(\vec{x} \mid y) \) นั้นไม่สามารถทำได้โดยตรงจากการแจงนับ ต้องมีการตั้งสมมุติฐานขึ้นมาก่อนเพื่อให้สามารถใช้กฏของความน่าจะเป็นได้เพื่อประมาณค่าได้
  3. เพื่อการ predict เราอาจละการทำ scaling หรือ การหารด้วย \(P(\vec{x}) \) ออกไปได้ เพราะไม่ได้ทำให้ความหมายเปลี่ยนแปลงในเชิงเปรียบเทียบ เช่น เราทราบว่า \( 9 > 6 \) เป็นจริง ในทำนองเดียวกันหากทำ scale ด้วย 3 , \( \frac{9}{3} > \frac{6}{3} \) ก็ยังเป็นจริงอยู่  ดังนั้น \[ P(y \mid \vec{x}) \approx P(y) \cdot P(\vec{x} \mid y) \tag{1.3} \]


สมมุติฐาน (Naive Assumption)

1. Independent : ภายใต้สมมุติฐานข้อนี้ให้ถือว่า \( x_1,x_2,x_3,...,x_j \) เป็นอิสระต่อกัน ไม่เป็นเงื่อนไขต่อกัน ผลคือทำให้นำเอาหลักการ probability dependency มาใช้ได้ [1]

2. Equal : ภายใต้สมมุติฐานข้อนี้ให้ถือว่า \( x_1,x_2,x_3,...,x_j \)  มีความสำคัญเท่ากัน หรือมีน้ำหนักเท่ากัน การคำนวณค่าความน่าจะเป็นของ \( P(y \mid \vec{x}) \) ต้องนำเอาค่าของทุก \(x_j\) มาคำนวณร่วมด้วย 

หมายเหตุ บางครั้งจะเห็นเรียกสมมุติฐาน 2 ข้อนี้ว่า naive Bayes assumption สมมุติฐานนี้ตั้งขึ้นเพื่อให้ง่ายต่อการคำนวณ ซึ่งอาจไม่ได้ผลในโลกความจริง


Conditional dependency

จากสมมุติฐานข้างต้นว่า การหาค่า \( P(\vec{x} \mid y) \)  ใน (1.3) หาได้จากหลักการของ conditional dependency [3] ที่ว่า 

เมื่อ \( x_1,x_2,x_3,...,x_j \) เป็นอิสระต่อกันแล้ว

\[ \begin{align*} P(x_1,x_2,x_3,...,x_j \mid y) &= P(x_1 \mid y) \cdot P(x_2 \mid y) \cdot P(x_3 \mid y) \cdots P(x_j \mid y) \\ P(\vec{x} \mid y) &= P(x_1 \mid y) \cdot P(x_2 \mid y) \cdot P(x_3 \mid y) \cdots P(x_j \mid y) \tag{1.4} \\ \end{align*} \]


นำ (1.4) ไปแทนใน (1.3) จะได้


\[ P(y \mid \vec{x}) \approx P(y) \cdot P(x_1 \mid y) \cdot P(x_2 \mid y) \cdots P(x_j \mid y) \tag{1.5} \]


ในความเป็นจริงแล้ว \( y_1,y_2,...,y_i \) ย่อมเป็นอิสระต่อกัน แต่ค่าของ \(x_j \) จะขึ้นกับ \(y_i \) ดังนั้นใน (1.5) จะต้องถูกคิดแยกกันของแต่ละ \(y_i\) 


\[ \begin{align*} P(y_i \mid \vec{x}_i ) &= P(y_i) \cdot P(x_i^1 \mid y_i) \cdot P(x^2_i \mid y_i) \cdot P(x^3_i \mid y_i) \cdots P(x^j_i \mid y_i) \tag{1.6} \\ \end{align*} \]

เมื่อ \( \vec{x}_i = (x^1_i,x^2_i,x^3_i,...,x^j_i) \)


รูปที่ 3


จากที่กล่าวมาอาจสรุปความเข้าใจดังนี้  สมมุติว่าข้อมูลที่จัดแบ่งเป็น 2 กลุ่ม \( y_1,y_2 \) โดยในแต่ละกลุ่มมี features \(x_1,x_2,x_3 \)เช่นเดียวกัน แต่มีการแจกแจงต่างกัน   (รูปที่ 3)  ค่าความน่าจะเป็นของแต่ละ features แทนด้วยขนาดของวงกลมภายในพื่้นที่ของแต่ละกลุ่ม


รูปที่ 4


ถ้าได้รับข้อมูลชิ้นใหม่เข้ามาเป็น \( (x_1^q,x_2^q,x_3^q)\)  และเรานำมาหาค่าความน่าจะเป็นเพื่อดูการแจกแจงในทั้งสองกลุ่ม (รูปที่ 4)  นำไปเทียบกับที่ทราบก่อนมาก่อนแล้ว (รูปที่ 3) จะเห็นว่า ข้อมูลชิ้นใหม่มีความน่าจะเป็นที่จะจัดอยู่กลุ่ม \( y_1\) มากกว่า \( y_2 \) ด้วยหลักคิดนี้ เราเรียกว่าการหา "maximum likelihood"[4]  

ในตอนนี้ได้กล่าวถึงภาคทฤษฎีที่โยงกันน่าจะครบแล้ว ตอนต่อไปจะนำเอาทฤษฎีไปสู่การปฏิบัติ ดูจาก ตัวอย่างที่ 1 และ ตัวอย่างที่ 2


ความคิดเห็น

แสดงความคิดเห็น